Pythagoras is said to have discovered the fact that two similar strings under the same tension and differing only in length, when sounded together give an effect that is pleasant to the ear if the lengths of the strings are in the ratio of two small integers. If the lengths are as, one is to two, they then correspond to the octave in music. If the lengths are as two is to three, they correspond to the interval between C and G, which is called a fifth. These intervals are generally accepted as “pleasant” sounding chords.

Pythagoras was so impressed by this discovery that he made it the basis of a school—Pythagoreans they were called—which held mystic beliefs in the great powers of numbers. It was believed that something similar would be found out about the planets—or “spheres.” We sometimes hear the expression: “the music of the spheres.” The idea was that there would be some numerical relationships between the orbits of the planets or between other things in nature. People usually think that this is just a kind of superstition held by the Greeks. But is it so different from our own scientific interest in quantitative relationships? Pythagoras’ discovery was the first example, outside geometry, of any numerical relationship in nature. It must have been very surprising to suddenly discover that there was a fact of nature that involved a simple numerical relationship. Simple measurements of lengths gave a prediction about something which had no apparent connection to geometry—the production of pleasant sounds. This discovery led to the extension that perhaps a good tool for understanding nature would be arithmetic and mathematical analysis. The results of modern science justify that point of view.

Pythagoras could only have made his discovery by making an experimental observation. Yet this important aspect does not seem to have impressed him. If it had, physics might have had a much earlier start. (It is always easy to look back at what someone else has done and to decide what he should have done!)

We might remark on a third aspect of this very interesting discovery: that the discovery had to do with two notes that sound pleasant to the ear. We may question whether we are any better off than Pythagoras in understanding why only certain sounds are pleasant to our ear. The general theory of aesthetics is probably no further advanced now than in the time of Pythagoras. In this one discovery of the Greeks, there are the three aspects: experiment, mathematical relationships, and aesthetics. Physics has made great progress on only the first two parts. This chapter will deal with our present-day understanding of the discovery of Pythagoras.

Among the sounds that we hear, there is one kind that we call noise. Noise corresponds to a sort of irregular vibration of the eardrum that is produced by the irregular vibration of some object in the neighborhood. If we make a diagram to indicate the pressure of the air on the eardrum (and, therefore, the displacement of the drum) as a function of time, the graph which corresponds to a noise might look like that shown in Fig. 50–1(a). (Such a noise might correspond roughly to the sound of a stamped foot.) The sound of music has a different character. Music is characterized by the presence of more-or-less sustained tones—or musical “notes.” (Musical instruments may make noises as well!) The tone may last for a relatively short time, as when a key is pressed on a piano, or it may be sustained almost indefinitely, as when a flute player holds a long note.

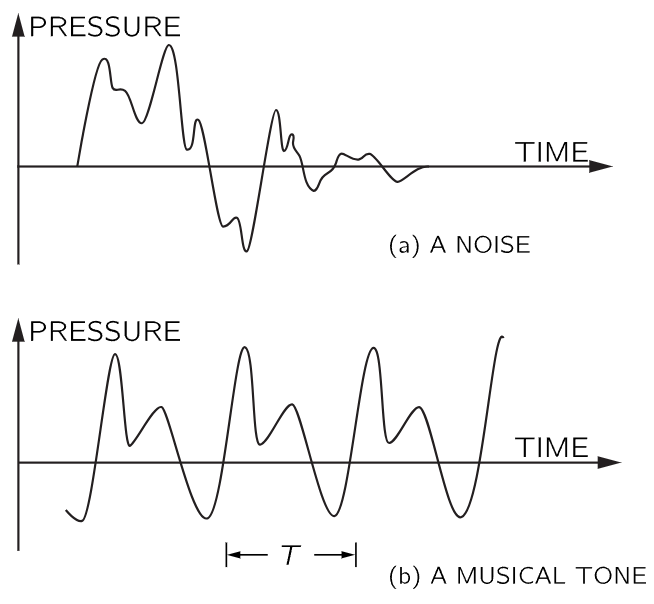
Fig. 50–1. Pressure as a function of time for (a) a noise, and (b) a musical tone.

What is the special character of a musical note from the point of view of the pressure in the air? A musical note differs from a noise in that there is a periodicity in its graph. There is some uneven shape to the variation of the air pressure with time, and the shape repeats itself over and over again. An example of a pressure-time function that would correspond to a musical note is shown in Fig. 50–1(b).

Musicians will usually speak of a musical tone in terms of three characteristics: the loudness, the pitch, and the “quality.” The “loudness” is found to correspond to the magnitude of the pressure changes. The “pitch” corresponds to the period of time for one repetition of the basic pressure function. (“Low” notes have longer periods than “high” notes.) The “quality” of a tone has to do with the differences we may still be able to hear between two notes of the same loudness and pitch. An oboe, a violin, or a soprano are still distinguishable even when they sound notes of the same pitch. The quality has to do with the structure of the repeating pattern.

Let us consider, for a moment, the sound produced by a vibrating string. If we pluck the string, by pulling it to one side and releasing it, the subsequent motion will be determined by the motions of the waves we have produced. We know that these waves will travel in both directions, and will be reflected at the ends. They will slosh back and forth for a long time. No matter how complicated the wave is, however, it will repeat itself. The period of repetition is just the time T required for the wave to travel two full lengths of the string. For that is just the time required for any wave, once started, to reflect off each end and return to its starting position, and be proceeding in the original direction. The time is the same for waves which start out in either direction. Each point on the string will, then, return to its starting position after one period, and again one period later, etc. The sound wave produced must also have the same repetition. We see why a plucked string produces a musical tone.