Let us now consider one more example of the phase velocity which is extremely interesting. It has to do with quantum mechanics. We know that the amplitude to find a particle at a place can, in some circumstances, vary in space and time, let us say in one dimension, in this manner:

where ω is the frequency, which is related to the classical idea of the energy through E=ℏω, and k is the wave number, which is related to the momentum through p=ℏk. We would say the particle had a definite momentum p if the wave number were exactly k, that is, a perfect wave which goes on with the same amplitude everywhere. Equation (48.19) gives the amplitude, and if we take the absolute square, we get the relative probability for finding the particle as a function of position and time. This is a constant, which means that the probability is the same to find a particle anywhere. Now suppose, instead, that we have a situation where we know that the particle is more likely to be at one place than at another. We would represent such a situation by a wave which has a maximum and dies out on either side (Fig. 48–6). (It is not quite the same as a wave like (48.1) which has a series of maxima, but it is possible, by adding several waves of nearly the same ω and k together, to get rid of all but one maximum.)

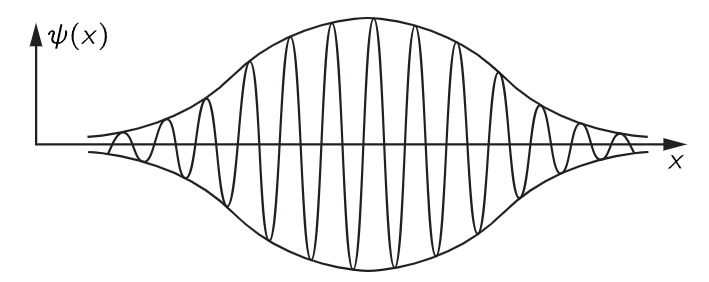
Fig. 48–6. A localized wave train.

Now in those circumstances, since the square of (48.19) represents the chance of finding a particle somewhere, we know that at a given instant the particle is most likely to be near the center of the “lump,” where the amplitude of the wave is maximum. If now we wait a few moments, the waves will move, and after some time the “lump” will be somewhere else. If we knew that the particle originally was situated somewhere, classically, we would expect that it would later be elsewhere as a matter of fact, because it has a speed, after all, and a momentum. The quantum theory, then, will go into the correct classical theory for the relationship of momentum, energy, and velocity only if the group velocity, the velocity of the modulation, is equal to the velocity that we would obtain classically for a particle of the same momentum.

It is now necessary to demonstrate that this is, or is not, the case. According to the classical theory, the energy is related to the velocity through an equation like

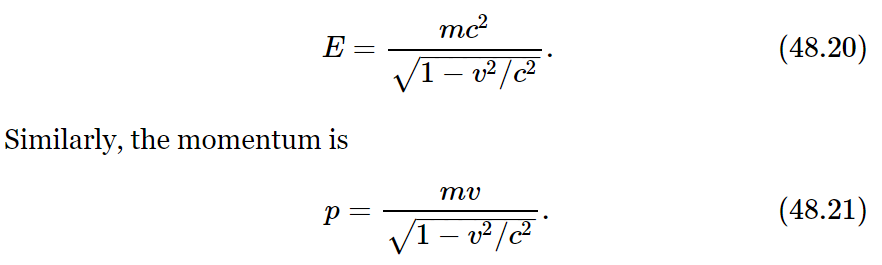
That is the classical theory, and as a consequence of the classical theory, by eliminating v, we can show that

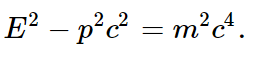
That is the four-dimensional grand result that we have talked and talked about, that p_μp_μ=m²; that is the relation between energy and momentum in the classical theory. Now that means, since these E’s and p’s are going to become ω’s and k’s, by substitution of E=ℏω and p=ℏk, that for quantum mechanics it is necessary that

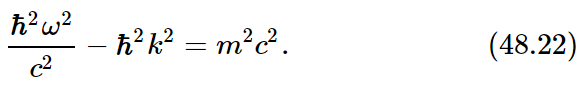
This, then, is the relationship between the frequency and the wave number of a quantum-mechanical amplitude wave representing a particle of mass m. From this equation we can deduce that ω is

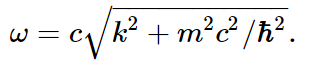
The phase velocity, ω/k, is here again faster than the speed of light!

Now let us look at the group velocity. The group velocity should be dω/dk, the speed at which the modulations move. We have to differentiate a square root, which is not very difficult. The derivative is

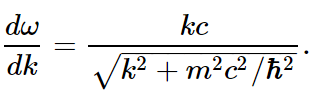
Now the square root is, after all, ω/c, so we could write this as dω/dk=c²k/ω. Further, k/ω is p/E, so

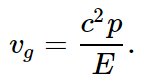
But from (48.20) and (48.21), c²p/E=v, the velocity of the particle, according to classical mechanics. So we see that whereas the fundamental quantum-mechanical relationship E=ℏω and p=ℏk, for the identification of ω and k with the classical E and p, only produces the equation ω²−k²c²=m²c⁴/ℏ², now we also understand the relationships (48.20) and (48.21) which connected E and p to the velocity. Of course, the group velocity must be the velocity of the particle if the interpretation is going to make any sense. If we think the particle is over here at one time, and then ten minutes later we think it is over there, as the quantum mechanics said, the distance traversed by the “lump,” divided by the time interval, must be, classically, the velocity of the particle.