Table 22–4

Successive Powers of 10^i/8

To further investigate the subject of taking complex imaginary powers, let us look at the powers of 10 taking successive powers, not doubling the power each time, in order to follow Table 22–3 further and to see what happens to those minus signs. This is shown in Table 22–4, in which we take 10^i/8, and just keep multiplying it. We see that x decreases, passes through zero, swings almost to −1 (if we could get in between p=10 and p=11 it would obviously swing to −1), and swings back. The y-value is going back and forth too.

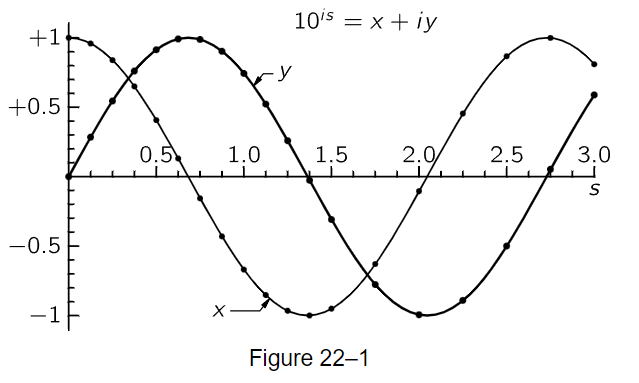
In Fig. 22–1 the dots represent the numbers that appear in Table 22–4, and the lines are just drawn to help you visually. So we see that the numbers x and y oscillate; 10^is repeats itself, it is a periodic thing, and as such, it is easy enough to explain, because if a certain power is i, then the fourth power of that would be i² squared. It would be +1 again, and therefore, since 10^0.68i is equal to i, by taking the fourth power we discover that 10^2.72i is equal to +1. Therefore, if we wanted 10^3.00i, for instance, we could write it as 10^2.72i times 10^0.28i. In other words, it has a period, it repeats. Of course, we recognize what the curves look like! They look like the sine and cosine, and we shall call them, for a while, the algebraic sine and algebraic cosine. However, instead of using the base 10, we shall put them into our natural base, which only changes the horizontal scale; so we denote 2.3025s by t, and write 10^is=e^it, where t is a real number. Now e^it=x+iy, and we shall write this as the algebraic cosine of t plus i times the algebraic sine of t. Thus

What are the properties of cos t and sin t? First, we know, for instance, that x²+y² must be 1; we have proved that before, and it is just as true for base e as for base 10. Therefore, cos ²t+sin ²t=1. We also know that, for small t, e^it=1+it, and therefore cos t is nearly 1, and sin t is nearly t, and so it goes, that all of the various properties of these remarkable functions, which come from taking imaginary powers, are the same as the sine and cosine of trigonometry.

Is the period the same? Let us find out. e to what power is equal to i? What is the logarithm of i to the base e? We worked it out before, in the base 10 it was 0.68184i, but when we change our logarithmic scale to e, we have to multiply by 2.3025, and if we do that it comes out 1.570. So this will be called “algebraic π/2.” But, we see, it differs from the regular π/2 by only one place in the last point, and that, of course, is the result of errors in our arithmetic! So we have created two new functions in a purely algebraic manner, the cosine and the sine, which belong to algebra, and only to algebra. We wake up at the end to discover the very functions that are natural to geometry. So there is a connection, ultimately, between algebra and geometry.

We summarize with this, the most remarkable formula in mathematics:

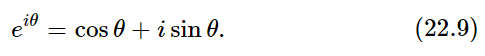
This is our jewel.

We may relate the geometry to the algebra by representing complex numbers in a plane; the horizontal position of a point is x, the vertical position of a point is y (Fig. 22–2). We represent every complex number, x+iy. Then if the radial distance to this point is called r and the angle is called θ, the algebraic law is that x+iy is written in the form re^iθ, where the geometrical relationships between x, y, r, and θ are as shown. This, then, is the unification of algebra and geometry.

Fig. 22–2.x+iy=re^iθ.

When we began this chapter, armed only with the basic notions of integers and counting, we had little idea of the power of the processes of abstraction and generalization. Using the set of algebraic “laws,” or properties of numbers, Eq. (22.1), and the definitions of inverse operations (22.2), we have been able here, ourselves, to manufacture not only numbers but useful things like tables of logarithms, powers, and trigonometric functions (for these are what the imaginary powers of real numbers are), all merely by extracting ten successive square roots of ten!