To illustrate another type of energy we consider a pendulum (Fig. 4–7). If we pull the mass aside and release it, it swings back and forth. In its motion, it loses height in going from either end to the center. Where does the potential energy go? Gravitational energy disappears when it is down at the bottom; nevertheless, it will climb up again. The gravitational energy must have gone into another form. Evidently it is by virtue of its motion that it is able to climb up again, so we have the conversion of gravitational energy into some other form when it reaches the bottom.

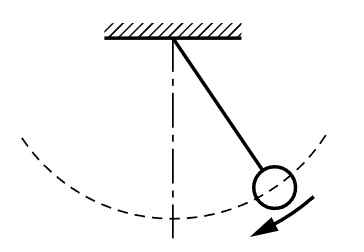
Fig. 4–7. Pendulum.

We must get a formula for the energy of motion. Now, recalling our arguments about reversible machines, we can easily see that in the motion at the bottom must be a quantity of energy which permits it to rise a certain height, and which has nothing to do with the machinery by which it comes up or the path by which it comes up. So we have an equivalence formula something like the one we wrote for the child’s blocks. We have another form to represent the energy. It is easy to say what it is. The kinetic energy at the bottom equals the weight times the height that it could go, corresponding to its velocity: K.E.=WH. What we need is the formula which tells us the height by some rule that has to do with the motion of objects. If we start something out with a certain velocity, say straight up, it will reach a certain height; we do not know what it is yet, but it depends on the velocity—there is a formula for that. Then to find the formula for kinetic energy for an object moving with velocity V, we must calculate the height that it could reach, and multiply by the weight. We shall soon find that we can write it this way:

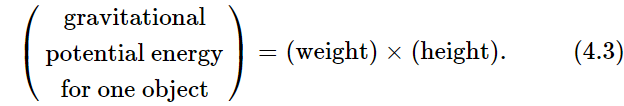
Of course, the fact that motion has energy has nothing to do with the fact that we are in a gravitational field. It makes no difference where the motion came from. This is a general formula for various velocities. Both (4.3) and (4.6) are approximate formulas, the first because it is incorrect when the heights are great, i.e., when the heights are so high that gravity is weakening; the second, because of the relativistic correction at high speeds. However, when we do finally get the exact formula for the energy, then the law of conservation of energy is correct.