Axiom of Extensionality

The axiom of Zermelo-Fraenkel set theory which asserts that sets formed by the same elements are equal,

Note that some texts (e.g., Devlin 1993), use a bidirectional equivalent 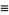 preceding "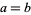," while others (e.g., Enderton 1977, Itô 1986), use the one-way implies 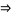. However, one-way implication suffices.

Using the notation 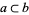 ( 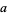is a subset of 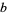) for 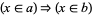, the axiom can be written concisely as

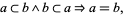where 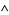 denotes logical AND.

REFERENCES:

Devlin, K. The Joy of Sets: Fundamentals of Contemporary Set Theory, 2nd ed. New York: Springer-Verlag, 1993.

Enderton, H. B. Elements of Set Theory. New York: Academic Press, 1977.

Itô, K. (Ed.). "Zermelo-Fraenkel Set Theory." §33B in Encyclopedic Dictionary of Mathematics, 2nd ed., Vol. 1. Cambridge, MA: MIT Press, pp. 147-148, 1986.