


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-10-2021
Date: 16-2-2016
Date: 23-12-2021
|
Define the "information function" to be
![I=-sum_(i=1)^NP_i(epsilon)ln[P_i(epsilon)],](https://mathworld.wolfram.com/images/equations/InformationDimension/NumberedEquation1.gif) |
(1) |
where 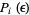 is the natural measure, or probability that element
is the natural measure, or probability that element 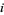 is populated, normalized such that
is populated, normalized such that
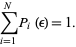 |
(2) |
The information dimension is then defined by
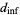 |
 |
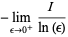 |
(3) |
 |
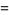 |
![lim_(epsilon->0^+)sum_(i=1)^(N)(P_i(epsilon)ln[P_i(epsilon)])/(ln(epsilon)).](https://mathworld.wolfram.com/images/equations/InformationDimension/Inline8.gif) |
(4) |
If every element is equally likely to be visited, then 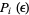 is independent of
is independent of 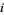 , and
, and
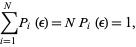 |
(5) |
so
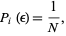 |
(6) |
and
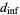 |
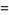 |
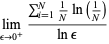 |
(7) |
 |
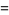 |
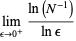 |
(8) |
 |
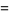 |
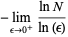 |
(9) |
 |
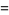 |
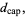 |
(10) |
where 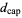 is the capacity dimension.
is the capacity dimension.
It satisfies
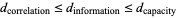 |
(11) |
where 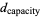 is the capacity dimension and
is the capacity dimension and 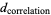 is the correlation dimension (correcting the typo in Baker and Gollub 1996).
is the correlation dimension (correcting the typo in Baker and Gollub 1996).
REFERENCES:
Baker, G. L. and Gollub, J. B. Chaotic Dynamics: An Introduction, 2nd ed. Cambridge, England: Cambridge University Press, 1996.
Balatoni, J. and Renyi, A. Pub. Math. Inst. Hungarian Acad. Sci. 1, 9, 1956.
Farmer, J. D. "Chaotic Attractors of an Infinite-dimensional Dynamical System." Physica D 4, 366-393, 1982.
Ott, E. Chaos in Dynamical Systems. New York: Cambridge University Press, p. 79, 1993.
Nayfeh, A. H. and Balachandran, B. Applied Nonlinear Dynamics: Analytical, Computational, and Experimental Methods. New York: Wiley, pp. 545-547, 1995.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|