Regular Space

According to most authors (e.g., Kelley 1955, p. 113; McCarty 1967, p. 144; Willard 1970, p. 92) a regular space is a topological space in which every neighborhood of a point contains a closed neighborhood of the same point.

Another equivalent condition is the following: for every closed set 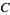 and every point  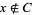there are two disjoint open sets  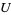and 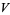 such that  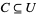and .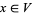

In other sources (e.g., Bourbaki 1989, p. 80; Cullen 1968, p. 113) regularity is defined differently, using separation axioms.

REFERENCES:

Bourbaki, N. "Regular Spaces." §1.4 in Elements of Mathematics: General Topology. Berlin: Springer-Verlag, pp. 80-81, 1989.

Cullen, H. F. "Regular Spaces." §17 in Introduction to General Topology. Boston, MA: Heath, pp. 113-118, 1968.

Kelley, J. L. General Topology. New York: Van Nostrand, 1955.

McCarty, G. "Regularity and 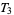-Spaces." In Topology, an Introduction. New York: McGraw-Hill, pp. 144-146, 1967.

Willard, S. "Regularity and Complete Regularity." §14 in General Topology. Reading, MA: Addison-Wesley, pp. 92-99, 1970.