Fibonorial

The fibonorial 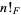, also called the Fibonacci factorial, is defined as

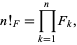where 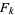 is a Fibonacci number. For 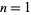, 2, ..., the first few fibonorials are 1, 1, 2, 6, 30, 240, 3120, 65520, ... (OEIS A003266).

The fibonorials are asymptotic to

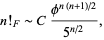where 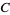 is the Fibonacci factorial constant and  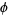is the golden ratio.

The first few values of 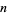 such that  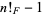is prime are given by 4, 5, 6, 7, 8, 14, 15, ... (OEIS A059709), with no others less than 500.

The first few values of 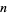 such that  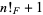is prime are given by 1, 2, 3, 4, 5, 6, 7, 8, 22, 28, ... (OEIS A053408), with no others less than 500.

REFERENCES:

Brousseau, A. Fibonacci and Related Number Theoretic Tables. San Jose, CA: Fibonacci Association, p. 69, 1972.

Finch, S. R. "Fibonacci Factorials." §1.2.5 in Mathematical Constants. Cambridge, England: Cambridge University Press, p. 10, 2003.

Graham, R. L.; Knuth, D. E.; and Patashnik, O. Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, p. 597, 1994.

Matiyasevich, Y. V. and Guy, R. K. "A New Formula for Pi." Amer. Math. Monthly 93, 631-635, 1986.

Sloane, N. J. A. Sequences A003266/M1692, A053408, and A059709 in "The On-Line Encyclopedia of Integer Sequences."