المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
{افان مات او قتل انقلبتم على اعقابكم}
2024-11-24
العبرة من السابقين
2024-11-24
تدارك الذنوب
2024-11-24
الإصرار على الذنب
2024-11-24
معنى قوله تعالى زين للناس حب الشهوات من النساء
2024-11-24
مسألتان في طلب المغفرة من الله
2024-11-24

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
الوصف النباتي للجوت والجلجل
2023-05-28
Coronal
4-7-2022
مدارس تحليل الخطاب
22-3-2022
فانيلين Biovanillin
1-9-2017
هل تباع المفترسات الحشرية لاستعمالها في مكافحة الآفات الحشرية؟
27-3-2021
الكثافة الإلكترونية electron density
18-12-2018

Species  
  
995   07:29 مساءً   date: 29-7-2021
Author : Bergeron, F.; Labelle, G.; and Leroux, P.
Book or Source : Combinatorial Species and Tree-Like Structures. Cambridge, England: Cambridge University Press
Page and Part : p. 5,


Read More
Submersion
Date: 13-7-2021 1857
Habiro Move
Date: 16-6-2021 1723
Fibration
Date: 24-5-2021 1368

Species

A species of structures is a rule 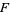F which

1. Produces, for each finite set 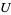U, a finite set F[U],

2. Produces, for each bijection 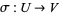sigma:U->V, a function

F[sigma]:F[U]->F[V].

(1)

The functions F[sigma] should further satisfy the following functorial properties:

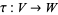1. For all bijections sigma:U->V and tau:V->W,

F[tau degreessigma]=F[tau] degreesF[sigma],

(2)

2. For the identity map 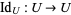Id_(U):U->U,

F[Id_(U)]=Id_(F[U]).

(3)

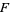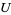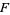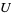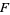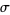An element sigma in F[U] is called an F-structure on U (or a structure of species F on U). The function F[sigma] is called the transport of F-structures along sigma.

REFERENCES:

Bergeron, F.; Labelle, G.; and Leroux, P. Combinatorial Species and Tree-Like Structures. Cambridge, England: Cambridge University Press, p. 5, 1998.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
التاريخ / 2024-11-23

الأخبار العلمية
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
التاريخ / 2024-11-23

الساحة الاسلامية
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
التاريخ / 2024-11-24