Tietze's Extension Theorem

A characterization of normal spaces with respect to the definition given by Kelley (1955, p. 112) or Willard (1970, p. 99). It states that the topological space 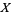 is normal iff, for all closed subsets  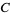of 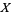, every continuous function 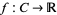, where  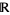denotes the real line with the Euclidean topology, can be extended to a continuous function  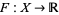(Willard 1970, p. 103).

With respect to the alternative definition (Cullen 1968, p. 118), the statement is different: if 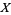 is a T4-space, for all closed subsets  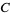of 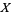, every continuous bounded function  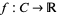can be extended to a continuous bounded function 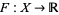. (Cullen 1968, p. 127)

Another characterization of normality in terms of maps is Urysohn's lemma.

REFERENCES:

Cullen, H. F. Introduction to General Topology. Boston, MA: Heath, 1968.

Joshi, K. D. "The Tietze Characterization of Normality." §7.44 in Introduction to General Topology. New Delhi, India: Wiley, pp. 182-188, 1983.

Kelley, J. L. General Topology. New York: Van Nostrand, 1955.

Willard, S. General Topology. Reading, MA: Addison-Wesley, pp. 99-108, 1970.