


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-7-2021
Date: 9-6-2021
Date: 13-7-2021
|
A connected set is a set that cannot be partitioned into two nonempty subsets which are open in the relative topology induced on the set. Equivalently, it is a set which cannot be partitioned into two nonempty subsets such that each subset has no points in common with the set closure of the other.
Let 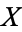 be a topological space. A connected set in
be a topological space. A connected set in 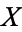 is a set
is a set 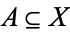 which cannot be partitioned into two nonempty subsets which are open in the relative topology induced on the set
which cannot be partitioned into two nonempty subsets which are open in the relative topology induced on the set 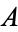 . Equivalently, it is a set which cannot be partitioned into two nonempty subsets such that each subset has no points in common with the set closure of the other. The space
. Equivalently, it is a set which cannot be partitioned into two nonempty subsets such that each subset has no points in common with the set closure of the other. The space 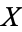 is a connected topological space if it is a connected subset of itself.
is a connected topological space if it is a connected subset of itself.
The real numbers are a connected set, as are any open or closed interval of real numbers. The (real or complex) plane is connected, as is any open or closed disc or any annulus in the plane. The topologist's sine curve is a connected subset of the plane. An example of a subset of the plane that is not connected is given by
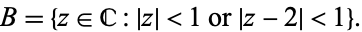 |
Geometrically, the set  is the union of two open disks of radius one whose boundaries are tangent at the number 1.
is the union of two open disks of radius one whose boundaries are tangent at the number 1.
REFERENCES:
Croft, H. T.; Falconer, K. J.; and Guy, R. K. Unsolved Problems in Geometry. New York: Springer-Verlag, p. 2, 1991.
Krantz, S. G. Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 3, 1999.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|