


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-5-2021
Date: 10-8-2021
Date: 14-7-2021
|
A Cartesian product of any finite or infinite set 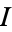 of copies of
of copies of 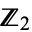 , equipped with the product topology derived from the discrete topology of
, equipped with the product topology derived from the discrete topology of 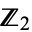 . It is denoted
. It is denoted 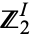 . The name is due to the fact that for
. The name is due to the fact that for 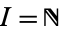 , this set is closely related to the Cantor set (which is formed by all numbers of the interval
, this set is closely related to the Cantor set (which is formed by all numbers of the interval ![[0,1]](https://mathworld.wolfram.com/images/equations/CantorsDiscontinuum/Inline6.gif) which admit an expansion in base 3 formed by 0s and 2s only), and this gives rise to a one-to-one correspondence between
which admit an expansion in base 3 formed by 0s and 2s only), and this gives rise to a one-to-one correspondence between 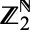 and the Cantor set, which is actually a homeomorphism. In the symbol denoting the Cantor discontinuum,
and the Cantor set, which is actually a homeomorphism. In the symbol denoting the Cantor discontinuum, 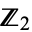 can be replaced by 2 and
can be replaced by 2 and 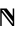 by
by 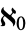 .
.
REFERENCES:
Cullen, H. F. "The Cantor Ternary Space." §18 in Introduction to General Topology. Boston, MA: Heath, pp. 77-81, 1968.
Joshi, K. D. Introduction to General Topology. New Delhi, India: Wiley, p. 199, 1983.
Willard, S. "The Cantor Set." §30 in General Topology. Reading, MA: Addison-Wesley, pp. 216-219, 1970.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|