Bridge Knot

An 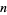-bridge knot is a knot with bridge number 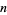. The set of 2-bridge knots is identical to the set of rational knots. If  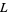is a 2-bridge knot, then the BLM/Ho polynomial  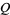and Jones polynomial  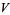satisfy

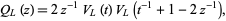where 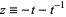 (Kanenobu and Sumi 1993). Kanenobu and Sumi also give a table containing the number of distinct 2-bridge knots of  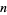crossings for  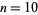to 22, both not counting and counting mirror images as distinct.

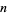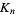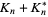3	0	0
4	0	0
5
6
7
8
9
10	45	85
11	91	182
12	176	341
13	352	704
14	693	1365
15	1387	2774
16	2752	5461
17	5504	11008
18	10965	21845
19	21931	43862
20	43776	87381
21	87552	175104
22	174933	349525

REFERENCES:

Kanenobu, T. and Sumi, T. "Polynomial Invariants of 2-Bridge Links through 20 Crossings." Adv. Studies Pure Math. 20, 125-145, 1992.

Kanenobu, T. and Sumi, T. "Polynomial Invariants of 2-Bridge Knots through 22-Crossings." Math. Comput. 60, 771-778 and S17-S28, 1993.

Schubert, H. "Knotten mit zwei Brücken." Math. Z. 65, 133-170, 1956.