Unknot

The unknot, also called the trivial knot (Rolfsen 1976, p. 51), is a closed loop that is not knotted. In the 1930s Reidemeister first proved that knots exist which are distinct from the unknot by inventing and making use of the so-called Reidemeister moves and coloring each part of a knot diagram with one of three colors.

The unknot is implemented in the Wolfram Language as KnotData["Unknot"].

The knot sum of two unknots is another unknot.

The Jones polynomial of the unknot is defined to give the normalization

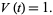(1)

The unknot has Alexander polynomial 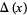 and Conway polynomial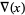 

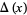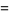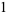			(2)
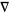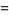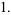			(3)

Surprisingly, there are known examples of nontrivial knots with Alexander polynomial 1, although no such examples occur among the knots of 10 or fewer crossings. An example is the 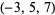-pretzel knot (Adams 1994, p. 167). Rolfsen (1976, p. 167) gives four other such examples.

Haken (1961) devised an algorithm to tell if a knot projection is the unknot. The algorithm is so complicated, however, that it has never been implemented.

REFERENCES:

Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 165-169, 1994.

Bar-Natan, D. "The Knot ." https://www.math.toronto.edu/~drorbn/KAtlas/Knots/0.1.html.

Haken, W. "Theorie der Normalflachen." Acta Math. 105, 245-375, 1961.

Livingston, C. Knot Theory. Washington, DC: Math. Assoc. Amer., p. 15, 1993.

Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, 1976.

Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 264-265, 1999.