


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-7-2021
Date: 21-6-2021
Date: 5-6-2021
|
For 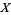 a topological space, the presheaf
a topological space, the presheaf 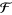 of Abelian groups (rings, ...) on
of Abelian groups (rings, ...) on 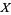 is defined such that
is defined such that
1. For every open subset 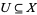 , an Abelian group (ring, ...)
, an Abelian group (ring, ...) 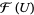 , and
, and
2. For every inclusion 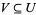 of open subsets of
of open subsets of 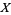 , a morphism of Abelian groups (rings, ...)
, a morphism of Abelian groups (rings, ...) 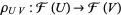
subject to the conditions:
1. If 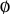 denotes the empty set, then
denotes the empty set, then 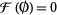 ,
,
2. 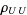 is the identity map
is the identity map 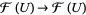 , and
, and
3. If 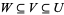 are three open subsets, then
are three open subsets, then 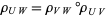 .
.
In the language of categories, let 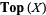 be the category whose objects are the open subsets of
be the category whose objects are the open subsets of 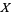 and the only morphisms are the inclusion maps. Thus,
and the only morphisms are the inclusion maps. Thus, 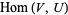 is empty if
is empty if 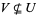 and
and 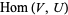 has just one element if
has just one element if 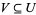 . Then a presheaf is a contravariant functor from the category
. Then a presheaf is a contravariant functor from the category 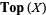 to the category
to the category 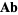 of Abelian groups (
of Abelian groups (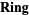 of rings, ...).
of rings, ...).
As a terminology, if 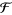 is a presheaf on
is a presheaf on 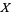 , then
, then 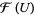 are called the sections of the presheaf over the open set
are called the sections of the presheaf over the open set 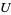 , sometimes denoted as
, sometimes denoted as 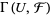 . The maps
. The maps 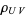 are called the restriction maps. If
are called the restriction maps. If 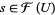 , then the notation
, then the notation 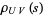 is usually used instead of
is usually used instead of 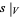 .
.
REFERENCES:
Hartshorne, R. Algebraic Geometry. Berlin: Springer-Verlag, pp. 60-61, 1977.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|