Homotopy Equivalence

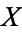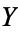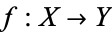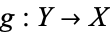Two topological spaces  and  are homotopy equivalent if there exist continuous maps  and , such that the composition  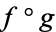is homotopic to the identity  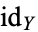on 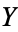, and such that  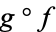is homotopic to 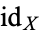. Each of the maps  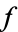and 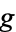 is called a homotopy equivalence, and  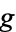is said to be a homotopy inverse to  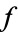(and vice versa).

One should think of homotopy equivalent spaces as spaces, which can be deformed continuously into one another.

Certainly any homeomorphism 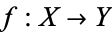 is a homotopy equivalence, with homotopy inverse 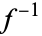, but the converse does not necessarily hold.

Some spaces, such as any ball 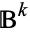, can be deformed continuously into a point. A space with this property is said to be contractible, the precise definition being that  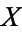is homotopy equivalent to a point. It is a fact that a space  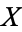is contractible, if and only if the identity map  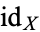is null-homotopic, i.e., homotopic to a constant map.