


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-1-2016
Date: 2-5-2021
Date: 8-2-2021
|
Let there be 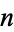 ways for a "good" selection and
ways for a "good" selection and 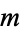 ways for a "bad" selection out of a total of
ways for a "bad" selection out of a total of 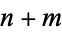 possibilities. Take
possibilities. Take 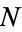 samples and let
samples and let 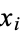 equal 1 if selection
equal 1 if selection 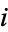 is successful and 0 if it is not. Let
is successful and 0 if it is not. Let 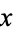 be the total number of successful selections,
be the total number of successful selections,
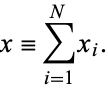 |
(1) |
The probability of 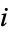 successful selections is then
successful selections is then
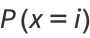 |
 |
![([# ways for i successes][# ways for N-i failures])/([total number of ways to select])](https://mathworld.wolfram.com/images/equations/HypergeometricDistribution/Inline11.gif) |
(2) |
 |
 |
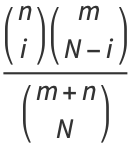 |
(3) |
 |
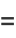 |
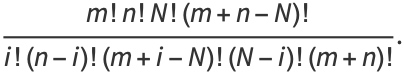 |
(4) |
The hypergeometric distribution is implemented in the Wolfram Language as HypergeometricDistribution[N, n, m+n].
The problem of finding the probability of such a picking problem is sometimes called the "urn problem," since it asks for the probability that 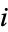 out of
out of 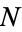 balls drawn are "good" from an urn that contains
balls drawn are "good" from an urn that contains 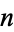 "good" balls and
"good" balls and 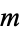 "bad" balls. It therefore also describes the probability of obtaining exactly
"bad" balls. It therefore also describes the probability of obtaining exactly 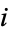 correct balls in a pick-
correct balls in a pick-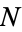 lottery from a reservoir of
lottery from a reservoir of 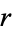 balls (of which
balls (of which 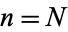 are "good" and
are "good" and 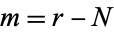 are "bad"). For example, for
are "bad"). For example, for 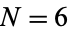 and
and 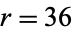 , the probabilities of obtaining
, the probabilities of obtaining 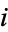 correct balls are given in the following table.
correct balls are given in the following table.
| number correct | probability | odds |
| 0 | 0.3048 | 2.280:1 |
| 1 | 0.4390 | 1.278:1 |
| 2 | 0.2110 | 3.738:1 |
| 3 | 0.04169 | 22.99:1 |
| 4 | 0.003350 | 297.5:1 |
| 5 | 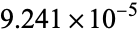 |
10820:1 |
| 6 | 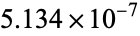 |
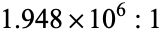 |
The 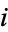 th selection has an equal likelihood of being in any trial, so the fraction of acceptable selections
th selection has an equal likelihood of being in any trial, so the fraction of acceptable selections 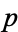 is
is
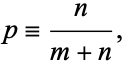 |
(5) |
i.e.,
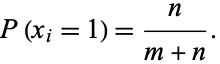 |
(6) |
The expectation value of 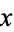 is therefore simply
is therefore simply
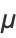 |
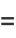 |
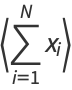 |
(7) |
 |
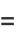 |
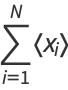 |
(8) |
 |
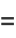 |
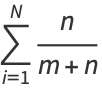 |
(9) |
 |
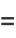 |
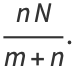 |
(10) |
This can also be computed by direct summation as
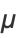 |
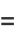 |
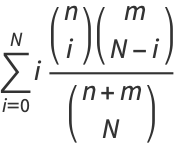 |
(11) |
 |
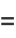 |
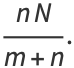 |
(12) |
The variance is
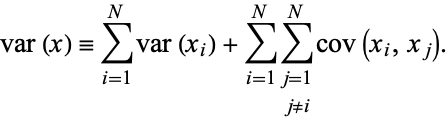 |
(13) |
Since 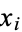 is a Bernoulli variable,
is a Bernoulli variable,
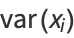 |
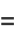 |
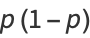 |
(14) |
 |
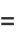 |
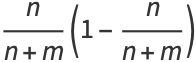 |
(15) |
 |
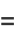 |
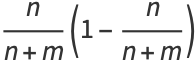 |
(16) |
 |
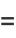 |
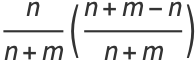 |
(17) |
 |
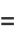 |
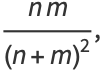 |
(18) |
so
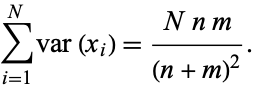 |
(19) |
For 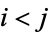 , the covariance is
, the covariance is
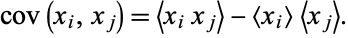 |
(20) |
The probability that both 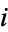 and
and 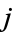 are successful for
are successful for 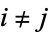 is
is
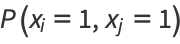 |
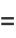 |
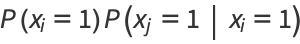 |
(21) |
 |
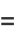 |
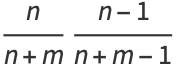 |
(22) |
 |
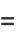 |
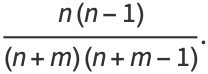 |
(23) |
But since 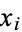 and
and 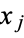 are random Bernoulli variables (each 0 or 1), their product is also a Bernoulli variable. In order for
are random Bernoulli variables (each 0 or 1), their product is also a Bernoulli variable. In order for 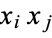 to be 1, both
to be 1, both 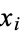 and
and 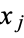 must be 1,
must be 1,
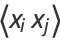 |
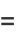 |
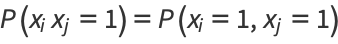 |
(24) |
 |
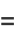 |
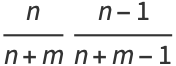 |
(25) |
 |
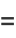 |
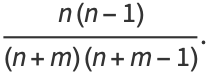 |
(26) |
Combining (26) with
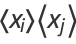 |
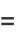 |
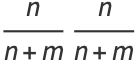 |
(27) |
 |
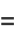 |
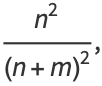 |
(28) |
gives
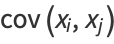 |
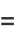 |
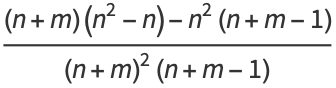 |
(29) |
 |
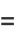 |
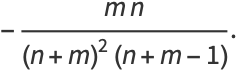 |
(30) |
There are a total of  terms in a double summation over
terms in a double summation over  . However,
. However,  for
for 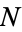 of these, so there are a total of
of these, so there are a total of 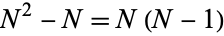 terms in the covariance summation
terms in the covariance summation
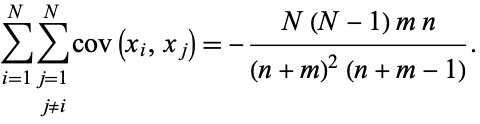 |
(31) |
Combining equations (◇), (◇), (◇), and (◇) gives the variance
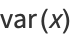 |
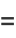 |
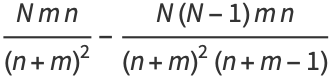 |
(32) |
 |
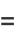 |
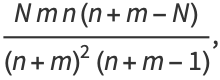 |
(33) |
so the final result is
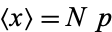 |
(34) |
and, since
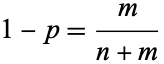 |
(35) |
and
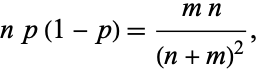 |
(36) |
we have
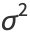 |
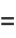 |
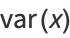 |
(37) |
 |
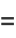 |
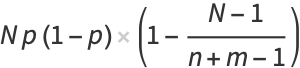 |
(38) |
 |
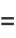 |
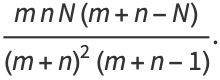 |
(39) |
This can also be computed directly from the sum
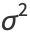 |
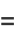 |
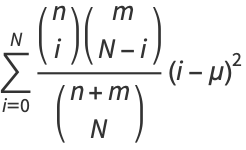 |
(40) |
 |
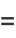 |
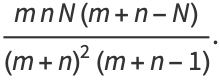 |
(41) |
The skewness is
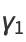 |
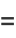 |
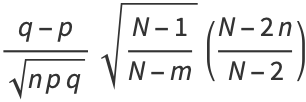 |
(42) |
 |
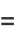 |
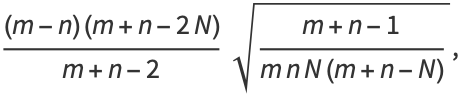 |
(43) |
and the kurtosis excess is given by a complicated expression.
The generating function is
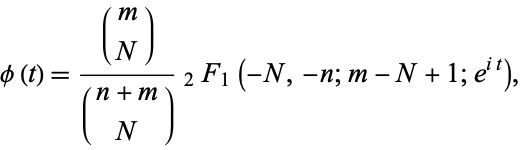 |
(44) |
where 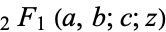 is the hypergeometric function.
is the hypergeometric function.
If the hypergeometric distribution is written
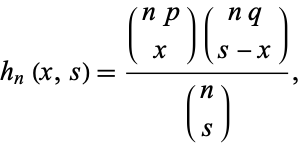 |
(45) |
then
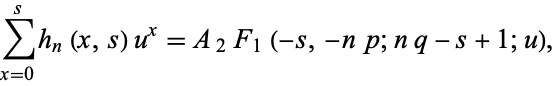 |
(46) |
where 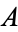 is a constant.
is a constant.
REFERENCES:
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 532-533, 1987.
Feller, W. "The Hypergeometric Series." §2.6 in An Introduction to Probability Theory and Its Applications, Vol. 1, 3rd ed. New York: Wiley, pp. 41-45, 1968.
Spiegel, M. R. Theory and Problems of Probability and Statistics. New York: McGraw-Hill, pp. 113-114, 1992.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة لجامعة سومر للمشاركة في حفل التخرج المركزي الخامس
|
|
|