


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-4-2021
Date: 3-5-2021
Date: 25-4-2021
|
The probability of getting at least one "6" in four rolls of a single 6-sided die is
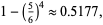 |
(1) |
which is slightly higher than the probability of at least one double-six in 24 throws of two dice,
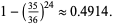 |
(2) |
The French nobleman and gambler Chevalier de Méré suspected that (1) was higher than (2), but his mathematical skills were not great enough to demonstrate why this should be so. He posed the question to Pascal, who solved the problem and proved de Méré correct. In fact, de Méré's observation remains true even if two dice are thrown 25 times, since the probability of throwing at least one double-six is then
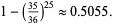 |
(3) |
REFERENCES:
Gonick, L. and Smith, W. The Cartoon Guide to Statistics. New York: Harper Perennial, pp. 28-29 and 44-45, 1993.
Kraitchik, M. "A Dice Problem." §6.2 in Mathematical Recreations. New York: W. W. Norton, pp. 118-119, 1942.
Uspensky, J. V. Introduction to Mathematical Probability. New York: McGraw-Hill, pp. 21-22, 1937.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة توجه دعوة لجامعة القادسية للمشاركة في حفل التخرج المركزي
|
|
|