Buffon-Laplace Needle Problem

The Buffon-Laplace needle problem asks to find the probability 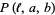 that a needle of length  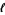will land on at least one line, given a floor with a grid of equally spaced parallel lines distances  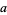and 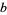 apart, with 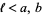. The position of the needle can be specified with points  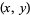and its orientation with coordinate 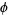. By symmetry, we can consider a single rectangle of the grid, so  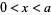and 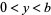. In addition, since opposite orientations are equivalent, we can take .

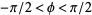The probability is given by

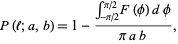(1)

where

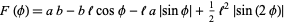(2)

(Uspensky 1937, p. 256; Solomon 1978, p. 4), giving

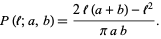(3)

This problem was first solved by Buffon (1777, pp. 100-104), but his derivation contained an error. A correct solution was given by Laplace (1812, pp. 359-362; Laplace 1820, pp. 365-369).

If 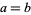 so that  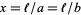and 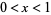, then the probabilities of a needle crossing 0, 1, and 2 lines are

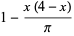			(4)
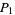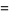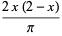			(5)
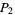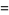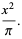			(6)

Defining 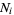 as the number of times in  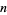tosses that a short needle crosses exactly  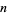lines, the variable  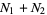has a binomial distribution with parameters  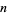and 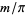, where  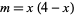(Perlman and Wichura 1975). A point estimator for  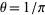is given by

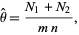(7)

which is a uniformly minimum variance unbiased estimator with variance

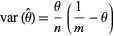(8)

(Perlman and Wishura 1975). An estimat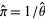or  for 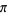 is then given by

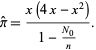(9)

This has asymptotic variance

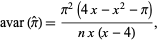(10)

which, for 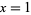, becomes

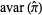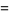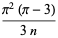			(11)
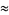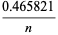			(12)

(OEIS A114602).

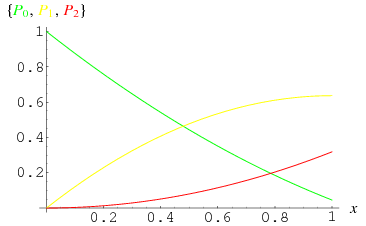
A set of sample trials is illustrated above for needles of length 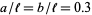, where needles intersecting 0 lines are shown in green, those intersecting a single line are shown in yellow, and those intersecting two lines are shown in red.

If the plane is instead tiled with congruent triangles with sides 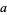, , 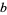, 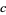and a needle with length  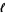less than the shortest altitude is thrown, the probability that the needle is contained entirely within one of the triangles is given by

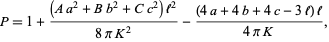(13)

where 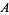, , 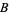and 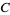 are the angles opposite 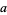, , 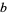and 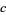, respectively, and  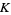is the area of the triangle. For a triangular grid consisting of equilateral triangles, this simplifies to

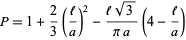(14)

(Markoff 1912, pp. 169-173; Uspensky 1937, p. 258).

REFERENCES:

Buffon, G. "Essai d'arithmétique morale." Histoire naturelle, générale er particulière, Supplément 4, 46-123, 1777.

Laplace, P. S. Théorie analytique des probabilités. Paris: Veuve Courcier, 1812.

Laplace, P. S. Théorie analytique des probabilités, 3rd rev. ed. Paris: Veuve Courcier, 1820.

Markoff, A. A. Wahrscheinlichkeitsrechnung. Leipzig, Germany: Teubner, 1912.

Perlman, M. and Wichura, M. "Sharpening Buffon's Needle." Amer. Stat. 20, 157-163, 1975.

Schuster, E. F. "Buffon's Needle Experiment." Amer. Math. Monthly 81, 26-29, 1974.

Sloane, N. J. A. Sequence A114602 in "The On-Line Encyclopedia of Integer Sequences."

Solomon, H. Geometric Probability. Philadelphia, PA: SIAM, pp. 3-6, 1978.

Uspensky, J. V. "Laplace's Problem." §12.17 in Introduction to Mathematical Probability. New York: McGraw-Hill, pp. 255-257, 1937.