Raw Moment

A moment 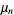 of a probability function  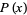taken about 0,

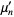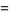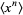			(1)
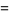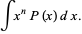			(2)

The raw moments 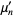 (sometimes also called "crude moments") can be expressed as terms of the central moments  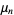(i.e., those taken about the mean 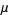) using the inverse binomial transform

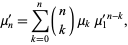(3)

with 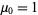 and 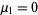 (Papoulis 1984, p. 146). The first few values are therefore

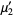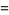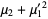			(4)
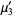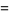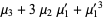			(5)
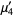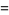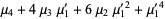			(6)
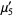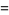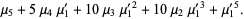			(7)

The raw moments 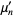 can also be expressed in terms of the cumulants  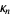by exponentiating both sides of the series

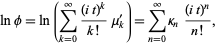(8)

where 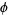 is the characteristic function, to obtain

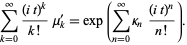(9)

The first few terms are then given by

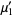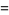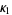			(10)
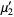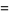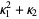			(11)
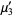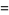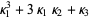			(12)
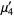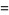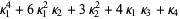			(13)
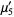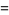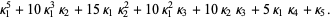			(14)

These transformations can be obtained using RawToCumulant[n] in the Mathematica application package mathStatica.

The raw moment of a multivariate probability function 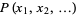 can be similarly defined as

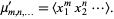(15)

Therefore,

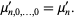(16)

The multivariate raw moments can be expressed in terms of the multivariate cumulants. For example,

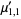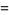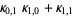			(17)
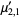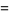			(18)

These transformations can be obtained using RawToCumulant[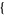m, n, ...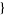] in the Mathematica application package mathStatica.

REFERENCES:

Kendall, M. G. "The Derivation of Multivariate Sampling Formulae from Univariate Formulae by Symbolic Operation." Ann. Eugenics 10, 392-402, 1940.

Kenney, J. F. and Keeping, E. S. "Moments About the Origin." §7.2 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 91-92, 1962.

Kratky, J.; Reinfelds, J.; Hutcheson, K.; and 47, L. R. "Tables of Crude Moments Expressed in Terms of Cumulants." Technical Report, University of Georgia, Athens, 1972.

Papoulis, A. Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, 1984.

Smith, P. J. "A Recursive Formulation of the Old Problem of Obtaining Moments from Cumulants and Vice Versa." Amer. Stat. 49, 217-218, 1995.