


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-5-2021
Date: 25-3-2021
Date: 6-2-2016
|
If 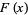 is a probability distribution with zero mean and
is a probability distribution with zero mean and
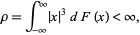 |
(1) |
where the above integral is a stieltjes integral, then for all  and
and 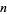 ,
,
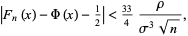 |
(2) |
where 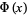 is the normal distribution function,
is the normal distribution function, 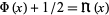 in Feller's notation, and
in Feller's notation, and
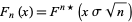 |
(3) |
is the normalized 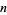 -fold convolution of
-fold convolution of 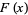 (Wallace 1958, Feller 1971).
(Wallace 1958, Feller 1971).
REFERENCES:
Bergström, H. "On the Central Limit Theorem." Skand. Aktuarietidskr. 27, 139-153, 1944.
Bergström, H. "On the Central Limit Theorem in the Space 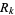 ,
, 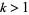 ." Skand. Aktuarietidskr. 28, 106-127, 1945.
." Skand. Aktuarietidskr. 28, 106-127, 1945.
Bergström, H. "On the Central Limit Theorem in the Case of not Equally Distributed Random Variables." Skand. Aktuarietidskr. 32, 37-62, 1949.
Berry, A. C. "The Accuracy of the Gaussian Approximation to the Sum of Independent Variates." Trans. Amer. Math. Soc. 49, 122-136 1941.
Esseen, C. G. "On the Liapounoff Limit of Error in the Theory of Probability." Ark. Mat. Astr. och Fys. 28A, No. 9, 1-19, 1942.
Esseen, C. G. "Fourier Analysis of Distribution Functions." Acta Math. 77, 1-125, 1945.
Esseen, C. G. "A Moment Inequality with an Application to the Central Limit Theorem." Skand. Aktuarietidskr. 39, 160-170, 1956.
Feller, W. "The Berry-Esséen Theorem." §16.5 in An Introduction to Probability Theory and Its Applications, Vol. 2, 3rd ed. New York: Wiley, pp. 542-546, 1971.
Hazewinkel, M. (Managing Ed.). Encyclopaedia of Mathematics: An Updated and Annotated Translation of the Soviet "Mathematical Encyclopaedia." Dordrecht, Netherlands: Reidel, p. 369, 1988.
Hsu, P. L. "The Approximate Distribution of the Mean and Variance of a Sample of Independent Variables." Ann. Math. Stat. 16, 1-29, 1945.
Wallace, D. L. "Asymptotic Approximations to Distributions." Ann. Math. Stat. 29, 635-654, 1958.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|