


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-3-2021
Date: 27-4-2021
Date: 7-2-2021
|
Maximum likelihood, also called the maximum likelihood method, is the procedure of finding the value of one or more parameters for a given statistic which makes the known likelihood distribution a maximum. The maximum likelihood estimate for a parameter 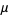 is denoted
is denoted 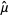 .
.
For a Bernoulli distribution,
![d/(dtheta)[(N; Np)theta^(Np)(1-theta)^(Nq)]=Np(1-theta)-thetaNq=0,](https://mathworld.wolfram.com/images/equations/MaximumLikelihood/NumberedEquation1.gif) |
(1) |
so maximum likelihood occurs for 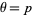 . If
. If 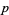 is not known ahead of time, the likelihood function is
is not known ahead of time, the likelihood function is
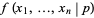 |
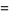 |
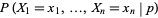 |
(2) |
 |
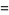 |
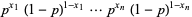 |
(3) |
 |
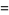 |
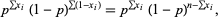 |
(4) |
where 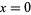 or 1, and
or 1, and 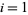 , ...,
, ..., 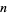 .
.
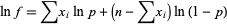 |
(5) |
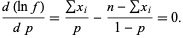 |
(6) |
Rearranging gives
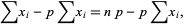 |
(7) |
so
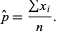 |
(8) |
For a normal distribution,
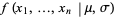 |
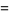 |
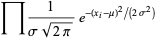 |
(9) |
 |
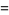 |
![((2pi)^(-n/2))/(sigma^n)exp[-(sum(x_i-mu)^2)/(2sigma^2)]](https://mathworld.wolfram.com/images/equations/MaximumLikelihood/Inline22.gif) |
(10) |
so
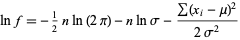 |
(11) |
and
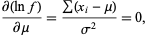 |
(12) |
giving
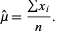 |
(13) |
Similarly,
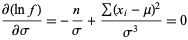 |
(14) |
gives
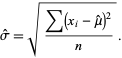 |
(15) |
Note that in this case, the maximum likelihood standard deviation is the sample standard deviation, which is a biased estimator for the population standard deviation.
For a weighted normal distribution,
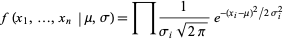 |
(16) |
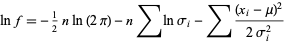 |
(17) |
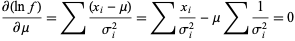 |
(18) |
gives
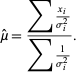 |
(19) |
The variance of the mean is then
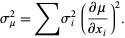 |
(20) |
But
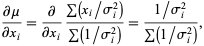 |
(21) |
so
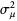 |
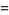 |
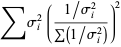 |
(22) |
 |
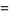 |
![sum(1/sigma_i^2)/([sum(1/sigma_i^2)]^2)](https://mathworld.wolfram.com/images/equations/MaximumLikelihood/Inline28.gif) |
(23) |
 |
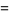 |
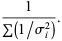 |
(24) |
For a Poisson distribution,
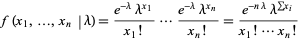 |
(25) |
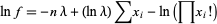 |
(26) |
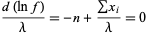 |
(27) |
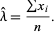 |
(28) |
REFERENCES:
Harris, J. W. and Stocker, H. "Maximum Likelihood Method." §21.10.4 in Handbook of Mathematics and Computational Science. New York: Springer-Verlag, p. 824, 1998.
Hoel, P. G. Introduction to Mathematical Statistics, 3rd ed. New York: Wiley, p. 57, 1962.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Least Squares as a Maximum Likelihood Estimator." §15.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 651-655, 1992.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
جمعية كشافة الكفيل تستعد لتقديم عرض مسرحي ضمن فعاليات حفل تخرج طلبة الجامعات
|
|
|