Semiprime

A semiprime, also called a 2-almost prime, biprime (Conway et al. 2008), or 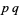-number, is a composite number that is the product of two (possibly equal) primes. The first few are 4, 6, 9, 10, 14, 15, 21, 22, ... (OEIS A001358). The first few semiprimes whose factors are distinct (i.e., the squarefree semiprimes) are 6, 10, 14, 15, 21, 22, 26, 33, 34, ... (OEIS A006881).

The square of any prime number is by definition a semiprime. The largest known semiprime is therefore the square of the largest known prime.

A formula for the number of semiprimes less than or equal to 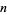 is given by

(1)

where 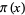 is the prime counting function and  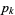is the 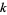th prime (R. G. Wilson V, pers. comm., Feb. 7, 2006; discovered independently by E. Noel and G. Panos around Jan. 2005, pers. comm., Jun. 13, 2006).

The numbers of semiprimes less than 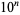 for 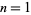, 2, ... are 3, 34, 299, 2625, 23378, 210035, ... (OEIS A066265).

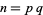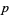For  with  and 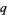 distinct, the following congruence is satisfied:

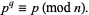(2)

In addition, the totient function satisfies the simple identity

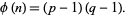(3)

Generating provable semiprimes of more than 250 digits by methods other than multiplying two primes together is nontrivial. One method is factorization. From the Cunningham project, 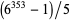 and 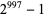 are factored semiprimes with 274 and 301 digits. In 2005, Don Reble showed how an elliptic pseudo-curve and the Goldwasser-Kilian ECPP theorem could generate a 1084-digit provable semiprime without a known factorization (Reble 2005).

Encryption algorithms such as RSA encryption rely on special large numbers that have as their factors two large primes. The following tables lists some special semiprimes that are the product of two large (distinct) primes.

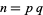	digits in	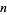digits in	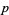digits in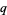
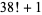	45	23	23
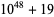	49	21	28
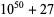	51	22	29
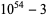	54	23	32
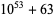	54	25	29
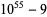	55	25	31
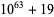	64	32	32
RSA-129	129	64	65
RSA-140	140	70	70
RSA-155	155	78	78

REFERENCES:

Conway, J. H.; Dietrich, H.; O'Brien, E. A. "Counting Groups: Gnus, Moas, and Other Exotica." Math. Intell. 30, 6-18, 2008.

Goldston, D. A.; Graham, S. W.; Pintz, J. and Yildirim, Y. "Small Gaps Between Primes or Almost Primes." 3 Jun 2005. https://arxiv.org/abs/math.NT/0506067.

Reble, D. "Interesting Semiprimes." https://www.graysage.com/djr/isp.txt.

Sloane, N. J. A. Sequences A001358/M3274, A0068814082, and A066265 in "The On-Line Encyclopedia of Integer Sequences."