


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-1-2021
Date: 20-8-2020
Date: 16-11-2020
|
The prime 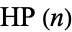 reached starting from a number
reached starting from a number 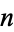 , concatenating its prime factors, and repeating until a prime is reached. For example, for
, concatenating its prime factors, and repeating until a prime is reached. For example, for 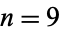 ,
,
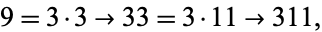 |
so 311 is the home prime of 9. For 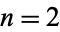 , 3, ..., the first few are 2, 3, 211, 5, 23, 7, 3331113965338635107, 311, 773, ... (OEIS A037274). Probabilistic arguments give exactly zero for the chance that the sequence of integers starting at a given number
, 3, ..., the first few are 2, 3, 211, 5, 23, 7, 3331113965338635107, 311, 773, ... (OEIS A037274). Probabilistic arguments give exactly zero for the chance that the sequence of integers starting at a given number 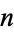 contains no prime, so a home prime should exist for every positive integer.
contains no prime, so a home prime should exist for every positive integer.
Since prime numbers have trivial home primes (themselves), attention can be restricted to composite numbers. The numbers of steps to arrive at a home prime for composite numbers 4, 6, 8, 9, ... are 2, 1, 13, 2, 4, 1, 5, 4, 4, 1, 15, 1, ... (OEIS A037271), and the primes they reach are 211, 23, 3331113965338635107, 311, 773, 223, ... (OEIS A037272).
The largest home prime for 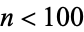 is
is 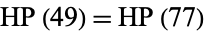 , although its value is not known. The first few terms in the home prime sequence for 49 are 49, 77, 711, 3379, 31109, 132393, 344131, ... (OEIS A056938). As of April 2011, computation of the sequence for this number is currently stalled at the 109th step on a 232-digit number which has yet to be completely factored.
, although its value is not known. The first few terms in the home prime sequence for 49 are 49, 77, 711, 3379, 31109, 132393, 344131, ... (OEIS A056938). As of April 2011, computation of the sequence for this number is currently stalled at the 109th step on a 232-digit number which has yet to be completely factored.
As of April 2011, there are 30 unknown 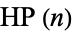 with
with 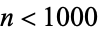 (excluding values of
(excluding values of 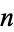 such as 77 which occur in the home prime sequence of a smaller number), the first few of which are 49, 146, 242, 312, 320, ... (Bonath).
such as 77 which occur in the home prime sequence of a smaller number), the first few of which are 49, 146, 242, 312, 320, ... (Bonath).
REFERENCES:
Bonath, K. "Open Sequences for Home Prime Base 10 (HP10) with 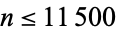 ." https://www.rieselprime.de/Others/HomePrime10.htm.
." https://www.rieselprime.de/Others/HomePrime10.htm.
De Geest, P. "Repeated Factorisation of Concatenated Primefactors of the Composite Numbers Up to 100 and Beyond..." https://www.worldofnumbers.com/topic1.htm.
Heleen, J. "Family Numbers: Constructing Primes by Prime Factor Splitting." J. Recr. Math. 28, 116-119, 1996-97.
MersenneWiki. "Base 10 Home Prime Results." https://www.mersennewiki.org/index.php/Base_10_Home_Prime_Results.
Sloane, N. J. A. Sequences A037271, A037272, A037273, A037274, and A056938 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|