Goldbach Number

A Goldbach number is a positive integer that is the sum of two odd primes (Li 1999). Let 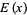 (the "exceptional set of Goldbach numbers") denote the number of even numbers not exceeding  which cannot be written as a sum of two odd primes. Then the Goldbach conjecture is equivalent to proving that 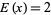 for every 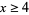. Li (1999) proved that for sufficiently large ,

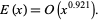REFERENCES:

Chen, J. R. "The Exceptional Set of Goldbach Numbers (II)." Sci. Sinica 26, 714-731, 1983.

Chen, J. R. and Liu, J. "The Exceptional Set of Goldbach Numbers (III)." Chinese Quart. J. Math. 4, 1-15, 1989.

Chen, J. R. and Pan, C. "The Exceptional Set of Goldbach Numbers." Sci. Sinica 23, 416-430, 1980.

Li, H. "The Exceptional Set of Goldbach Numbers." Quart. J. Math. Oxford 50, 471-482, 1999.

Montgomery, H. L. and Vaughan, R. C. "The Exceptional Set of Goldbach's Problem." Acta. Arith. 27, 353-370, 1975.