المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Morgado Identity |
 602
 02:57 صباحاً
date: 7-12-2020 |
Author : Dujella, A. 
Book or Source : "Diophantine Quadruples for Squares of Fibonacci and Lucas Numbers." Portugaliae Math. 52 
Page and Part : ...|
Read More
Date: 2-3-2020
538
Date: 18-12-2020
822
Date: 27-11-2019
777
|
There are several results known as the Morgado identity. The first is
![F_nF_(n+1)F_(n+2)F_(n+4)F_(n+5)F_(n+6)+L_(n+3)^2=[F_(n+3)(2F_(n+2)F_(n+4)-F_(n+3)^2)]^2,](https://mathworld.wolfram.com/images/equations/MorgadoIdentity/NumberedEquation1.gif) |
(1) |
where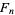 
is a Fibonacci number and 
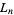is a Lucas number (Morgado 1987, Dujella 1995).
A second Morgado identity is satisfied by generalized Fibonacci numbers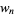 
,
 |
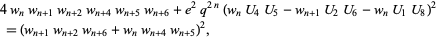(2) |
where
 |
 |
 |
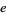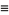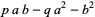(3) |
 |
 |
 |
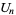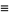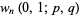(4) |
(Morgado 1987, Dujella 1996).
REFERENCES:
Dujella, A. "Diophantine Quadruples for Squares of Fibonacci and Lucas Numbers." Portugaliae Math. 52, 305-318, 1995.
Dujella, A. "Generalized Fibonacci Numbers and the Problem of Diophantus." Fib. Quart. 34, 164-175, 1996.
Morgado, J. "Note on Some Results of A. F. Horadam and A. G. Shannon Concerning a Catalan's Identity on Fibonacci Numbers." Portugaliae Math. 44, 243-252, 1987.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
