المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Multiamicable Numbers |
 884
 03:16 مساءً
date: 26-11-2020 |
Author : Cohen, G. L; Gretton, S.; and Hagis, P. Jr 
Book or Source : "Multiamicable Numbers." Math. Comput. 64 
Page and Part : ...|
Read More
Date: 25-1-2021
690
Date: 2-11-2019
758
Date: 14-10-2020
665
|
Two integers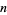 
and 
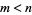are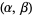 
-multiamicable if
 |
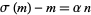and
 |
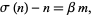where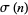 
is the divisor function and 
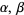are positive integers. If 
, 
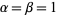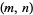is an amicable pair.
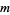cannot have just one distinct prime factor, and if it has precisely two distinct prime factors, then 
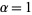and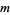 
is even. Small multiamicable numbers for small 
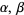are given by Cohen et al. (1995). Several of these numbers are reproduced in the table below.
 |
 |
 |
 |
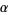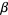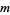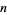| 1 | 6 | 76455288 | 183102192 |
| 1 | 7 | 52920 | 152280 |
| 1 | 7 | 16225560 | 40580280 |
| 1 | 7 | 90863136 | 227249568 |
| 1 | 7 | 16225560 | 40580280 |
| 1 | 7 | 70821324288 | 177124806144 |
| 1 | 7 | 199615613902848 | 499240550375424 |
REFERENCES:
Cohen, G. L; Gretton, S.; and Hagis, P. Jr. "Multiamicable Numbers." Math. Comput. 64, 1743-1753, 1995.ش
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
