


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 14-11-2019
Date: 21-9-2020
Date: 19-3-2020
|
Let ![[a_0;a_1,a_2,...]](http://mathworld.wolfram.com/images/equations/KhinchinHarmonicMean/Inline1.gif) be the simple continued fraction of a "generic" real number, where the numbers
be the simple continued fraction of a "generic" real number, where the numbers 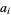 are the partial quotients. Then the Khinchin (or Khintchine) harmonic mean
are the partial quotients. Then the Khinchin (or Khintchine) harmonic mean
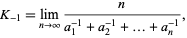 |
(1) |
defined analogously to the Khinchin constant  but with the partial quotients taken to the
but with the partial quotients taken to the  power, exists and has a unique common value (except for a set of real numbers with measure zero) given by
power, exists and has a unique common value (except for a set of real numbers with measure zero) given by
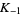 |
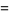 |
![ln2[sum_(n=1)^(infty)ln(1-1/((n+1)^2))^(-1/n)]^(-1)](http://mathworld.wolfram.com/images/equations/KhinchinHarmonicMean/Inline7.gif) |
(2) |
 |
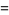 |
![-ln2[sum_(n=1)^(infty)1/nln(1-1/((n+1)^2))]^(-1)](http://mathworld.wolfram.com/images/equations/KhinchinHarmonicMean/Inline10.gif) |
(3) |
 |
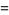 |
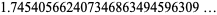 |
(4) |
(OEIS A087491; Bailey et al. 1997, Plouffe).
Khinchin's constant 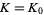 and the Khinchin harmonic mean
and the Khinchin harmonic mean 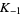 are just two of an infinite family of such constants
are just two of an infinite family of such constants 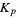 , the first few of which are summarized in the following table.
, the first few of which are summarized in the following table.
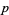 |
OEIS | value |
| 0 | A002210 | 2.685452001065306445309714835481795693820382293994462 |
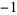 |
A087491 | 1.745405662407346863494596309683661067294936618777984 |
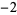 |
A087492 | 1.450340328495630406052983076680697881408299979605904 |
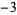 |
A087493 | 1.313507078687985766717339447072786828158129861484792 |
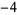 |
A087494 | 1.236961809423730052626227244453422567420241131548937 |
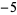 |
A087495 | 1.189003926465513154062363732771403397386092512639671 |
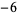 |
A087496 | 1.156552374421514423152605998743410046840213070718761 |
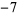 |
A087497 | 1.133323363950865794910289694908868363599098282411797 |
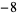 |
A087498 | 1.115964408978716690619156419345349695769491182230400 |
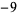 |
A087499 | 1.102543136670728013836093402522568351022221284149318 |
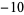 |
A087500 | 1.091877041209612678276110979477638256493272651429656 |
REFERENCES:
Bailey, D. H.; Borwein, J. M.; and Crandall, R. E. "On the Khintchine Constant." Math. Comput. 66, 417-431, 1997.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 161, 2003.
Khinchin, A. Ya. "Average Values." §16 in Continued Fractions. New York: Dover, pp. 86-94, 1997.
Plouffe, S. "The Khintchine Harmonic Mean." http://pi.lacim.uqam.ca/piDATA/khintchine1.txt.
Sloane, N. J. A. Sequence A087491 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
دورة تدريبية بعنوان ..فن إدارة الوقت
|
|
|