Aliquot Sequence

Let

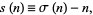where 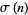 is the divisor function and  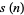is the restricted divisor function. Then the sequence of numbers

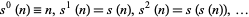is called an aliquot sequence. If the sequence for a given 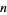 is bounded, it either ends at  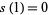or becomes periodic.

1. If the sequence reaches a constant, the constant is known as a perfect number. A number that is not perfect, but for which the sequence becomes constant, is known as an aspiring number.

2. If the sequence reaches an alternating pair, it is called an amicable pair.

3. If, after 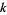 iterations, the sequence yields a cycle of minimum length  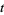of the form 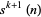, , 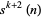..., 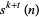, then these numbers form a group of sociable numbers of order .

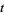The lengths of the aliquot sequences for 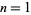, 2, ... are 1, 2, 2, 3, 2, 1, 2, 3, 4, 4, 2, 7, 2, 5, 5, 6, 2, ... (OEIS A044050).

It has not been proven that all aliquot sequences eventually terminate and become periodic. The smallest number whose fate is not known is 276. Guy (1994) cites the largest computed value as 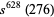, though this has since been extended to  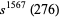(Zimmermann 2008). There are five such sequences less than 1000, namely 276, 552, 564, 660, and 966 (Clavier 2006, Varona 2004), sometimes called the "Lehmer five" (Zimmermann 2008). Furthermore, there are 81 open sequences 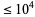, 908 open sequences 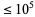, and 9452 open sequences  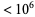(Creyaufmüller 2008).

REFERENCES:

Clavier, C. "Aliquot Sequences." May 28, 2008. https://christophe.clavier.free.fr/Aliquot/site/Aliquot.html.

Clavier, C. "Aliquot Sequences 276, 552, 564, 660, 996, 1074 and 1134 Pursued by Paul Zimmermann." Dec. 17, 2006. https://christophe.clavier.free.fr/Aliquot/site/zimmermann_table.html.

Creyaufmüller, W. "Aliquot Sequences." May 13, 2008. https://www.aliquot.de/aliquote.htm#aliquot%20sequences.

Guy, R. K. "Aliquot Sequences." §B6 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 60-62, 1994.

Guy, R. K. and Selfridge, J. L. "What Drives Aliquot Sequences." Math. Comput. 29, 101-107, 1975.

Sloane, N. J. A. Sequences A003023/M0062 and A044050 in "The On-Line Encyclopedia of Integer Sequences."

Sloane, N. J. A. and Plouffe, S. Figure M0062 in The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.

Varona, J. L. "Aliquot Sequences." Sep. 16, 2004. https://www.unirioja.es/dptos/dmc/jvarona/aliquot.html.

Zimmermann, P. "Aliquot Sequences." Retrieved Jun. 1, 2008. https://www.loria.fr/~zimmerma/records/aliquot.html.