


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-8-2020
Date: 15-3-2020
Date: 11-2-2020
|
Start with an integer 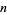 , known as the digitaddition generator. Add the sum of the digitaddition generator's digits to obtain the digitaddition
, known as the digitaddition generator. Add the sum of the digitaddition generator's digits to obtain the digitaddition 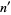 . A number can have more than one digitaddition generator. If a number has no digitaddition generator, it is called a self number. The sum of all numbers in a digitaddition series is given by the last term minus the first plus the sum of the digits of the last.
. A number can have more than one digitaddition generator. If a number has no digitaddition generator, it is called a self number. The sum of all numbers in a digitaddition series is given by the last term minus the first plus the sum of the digits of the last.
If the digitaddition process is performed on 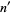 to yield its digitaddition
to yield its digitaddition 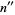 , on
, on 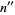 to yield
to yield 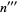 , etc., a single-digit number, known as the digital root of
, etc., a single-digit number, known as the digital root of 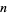 , is eventually obtained. The digital roots of the first few integers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, ... (OEIS A010888).
, is eventually obtained. The digital roots of the first few integers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, 2, 3, 4, 5, 6, 7, 8, 9, 1, ... (OEIS A010888).
If the process is generalized so that the 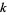 th (instead of first) powers of the digits of a number are repeatedly added, a periodic sequence of numbers is eventually obtained for any given starting number
th (instead of first) powers of the digits of a number are repeatedly added, a periodic sequence of numbers is eventually obtained for any given starting number 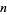 . For example, the 2-digitaddition sequence for
. For example, the 2-digitaddition sequence for 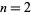 is given by 2,
is given by 2, 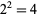 ,
, 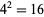 ,
, 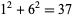 ,
, 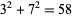 ,
, 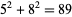 ,
, 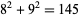 , and so on.
, and so on.
If the original number 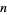 is equal to the sum of the
is equal to the sum of the 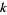 th powers of its digits (i.e., the digitaddition sequence has length 2),
th powers of its digits (i.e., the digitaddition sequence has length 2), 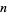 is called a Narcissistic number. If the original number is the smallest number in the eventually periodic sequence of numbers in the repeated
is called a Narcissistic number. If the original number is the smallest number in the eventually periodic sequence of numbers in the repeated 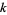 -digitadditions, it is called a recurring digital invariant. Both Narcissistic numbers and recurring digital invariants are relatively rare.
-digitadditions, it is called a recurring digital invariant. Both Narcissistic numbers and recurring digital invariants are relatively rare.
The only possible periods for repeated 2-digitadditions are 1 and 8, and the periods of the first few positive integers are 1, 8, 8, 8, 8, 8, 1, 8, 8, 1, ... (OEIS A031176). Similarly, the numbers that correspond to the beginning of the eventually periodic part of a 2-digitaddition sequence are given by 1, 4, 37, 4, 89, 89, 1, 89, 37, 1, 4, ... (OEIS A103369).
The possible periods 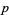 for
for 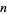 -digitadditions are summarized in the following table, together with digitadditions for the first few integers and the corresponding sequence numbers. Some periods do not show up for a long time. For example, a period-6 10-digitaddition does not occur until the number 266.
-digitadditions are summarized in the following table, together with digitadditions for the first few integers and the corresponding sequence numbers. Some periods do not show up for a long time. For example, a period-6 10-digitaddition does not occur until the number 266.
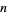 |
OEIS | 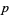 s s |
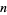 -digitadditions -digitadditions |
| 2 | A031176 | 1, 8 | 1, 8, 8, 8, 8, 8, 1, 8, 8, 1, ... |
| 3 | A031178 | 1, 2, 3 | 1, 1, 1, 3, 1, 1, 1, 1, 1, 1, 1, 1, 3, ... |
| 4 | A031182 | 1, 2, 7 | 1, 7, 7, 7, 7, 7, 7, 7, 7, 1, 7, 1, 7, 7, ... |
| 5 | A031186 | 1, 2, 4, 6, 10, 12, 22, 28 | 1, 12, 22, 4, 10, 22, 28, 10, 22, 1, ... |
| 6 | A031195 | 1, 2, 3, 4, 10, 30 | 1, 10, 30, 30, 30, 10, 10, 10, 3, 1, 10, ... |
| 7 | A031200 | 1, 2, 3, 6, 12, 14, 21, 27, 30, 56, 92 | 1, 92, 14, 30, 92, 56, 6, 92, 56, 1, 92, 27, ... |
| 8 | A031211 | 1, 25, 154 | 1, 25, 154, 154, 154, 154, 25, 154, 154, 1, 25, 154, 154, 1, ... |
| 9 | A031212 | 1, 2, 3, 4, 8, 10, 19, 24, 28, 30, 80, 93 | 1, 30, 93, 1, 19, 80, 4, 30, 80, 1, 30, 93, 4, 10, ... |
| 10 | A031213 | 1, 6, 7, 17, 81, 123 | 1, 17, 123, 17, 17, 123, 123, 123, 123, 1, 17, 123, 17, ... |
The numbers having period-1 2-digitaddition sequences are also called happy numbers, the first few of which are 1, 7, 10, 13, 19, 23, 28, 31, 32, ... (OEIS A007770).
The first few numbers having period 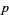
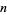 -digitadditions are summarized in the following table.
-digitadditions are summarized in the following table.
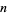 |
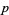 |
OEIS | members |
| 2 | 1 | A007770 | 1, 7, 10, 13, 19, 23, 28, 31, 32, ... |
| 2 | 8 | A031177 | 2, 3, 4, 5, 6, 8, 9, 11, 12, 14, 15, ... |
| 3 | 1 | A031179 | 1, 2, 3, 5, 6, 7, 8, 9, 10, 11, 12, ... |
| 3 | 2 | A031180 | 49, 94, 136, 163, 199, 244, 316, ... |
| 3 | 3 | A031181 | 4, 13, 16, 22, 25, 28, 31, 40, 46, ... |
| 4 | 1 | A031183 | 1, 10, 12, 17, 21, 46, 64, 71, 100, ... |
| 4 | 2 | A031184 | 66, 127, 172, 217, 228, 271, 282, ... |
| 4 | 7 | A031185 | 2, 3, 4, 5, 6, 7, 8, 9, 11, 13, 14, ... |
| 5 | 1 | A031187 | 1, 10, 100, 145, 154, 247, 274, ... |
| 5 | 2 | A031188 | 133, 139, 193, 199, 226, 262, ... |
| 5 | 4 | A031189 | 4, 37, 40, 55, 73, 124, 142, ... |
| 5 | 6 | A031190 | 16, 61, 106, 160, 601, 610, 778, ... |
| 5 | 10 | A031191 | 5, 8, 17, 26, 35, 44, 47, 50, 53, ... |
| 5 | 12 | A031192 | 2, 11, 14, 20, 23, 29, 32, 38, 41, ... |
| 5 | 22 | A031193 | 3, 6, 9, 12, 15, 18, 21, 24, 27, ... |
| 5 | 28 | A031194 | 7, 13, 19, 22, 25, 28, 31, 34, 43, ... |
| 6 | 1 | A011557 | 1, 10, 100, 1000, 10000, 100000, ... |
| 6 | 2 | A031357 | 3468, 3486, 3648, 3684, 3846, ... |
| 6 | 3 | A031196 | 9, 13, 31, 37, 39, 49, 57, 73, 75, ... |
| 6 | 4 | A031197 | 255, 466, 525, 552, 646, 664, ... |
| 6 | 10 | A031198 | 2, 6, 7, 8, 11, 12, 14, 15, 17, 19, ... |
| 6 | 30 | A031199 | 3, 4, 5, 16, 18, 22, 29, 30, 33, ... |
| 7 | 1 | A031201 | 1, 10, 100, 1000, 1259, 1295, ... |
| 7 | 2 | A031202 | 22, 202, 220, 256, 265, 526, 562, ... |
| 7 | 3 | A031203 | 124, 142, 148, 184, 214, 241, 259, ... |
| 7 | 6 | 7, 70, 700, 7000, 70000, 700000, ... | |
| 7 | 12 | A031204 | 17, 26, 47, 59, 62, 71, 74, 77, 89, ... |
| 7 | 14 | A031205 | 3, 30, 111, 156, 165, 249, 294, ... |
| 7 | 21 | A031206 | 19, 34, 43, 91, 109, 127, 172, 190, ... |
| 7 | 27 | A031207 | 12, 18, 21, 24, 39, 42, 45, 54, 78, ... |
| 7 | 30 | A031208 | 4, 13, 16, 25, 28, 31, 37, 40, 46, ... |
| 7 | 56 | A031209 | 6, 9, 15, 27, 33, 36, 48, 51, 57, ... |
| 7 | 92 | A031210 | 2, 5, 8, 11, 14, 20, 23, 29, 32, 35, ... |
| 8 | 1 | 1, 10, 14, 17, 29, 37, 41, 71, 73, ... | |
| 8 | 25 | 2, 7, 11, 15, 16, 20, 23, 27, 32, ... | |
| 8 | 154 | 3, 4, 5, 6, 8, 9, 12, 13, 18, 19, ... | |
| 9 | 1 | 1, 4, 10, 40, 100, 400, 1000, 1111, ... | |
| 9 | 2 | 127, 172, 217, 235, 253, 271, 325, ... | |
| 9 | 3 | 444, 4044, 4404, 4440, 4558, ... | |
| 9 | 4 | 7, 13, 31, 67, 70, 76, 103, 130, ... | |
| 9 | 8 | 22, 28, 34, 37, 43, 55, 58, 73, 79, ... | |
| 9 | 10 | 14, 38, 41, 44, 83, 104, 128, 140, ... | |
| 9 | 19 | 5, 26, 50, 62, 89, 98, 155, 206, ... | |
| 9 | 24 | 16, 61, 106, 160, 337, 373, 445, ... | |
| 9 | 28 | 19, 25, 46, 49, 52, 64, 91, 94, ... | |
| 9 | 30 | 2, 8, 11, 17, 20, 23, 29, 32, 35, ... | |
| 9 | 80 | 6, 9, 15, 18, 24, 33, 42, 48, 51, ... | |
| 9 | 93 | 3, 12, 21, 27, 30, 36, 39, 45, 54, ... | |
| 10 | 1 | A011557 | 1, 10, 100, 1000, 10000, 100000, ... |
| 10 | 6 | 266, 626, 662, 1159, 1195, 1519, ... | |
| 10 | 7 | 46, 58, 64, 85, 122, 123, 132, ... | |
| 10 | 17 | 2, 4, 5, 11, 13, 20, 31, 38, 40, ... | |
| 10 | 81 | 17, 18, 37, 71, 73, 81, 107, 108, ... | |
| 10 | 123 | 3, 6, 7, 8, 9, 12, 14, 15, 16, 19, ... |
REFERENCES:
Sloane, N. J. A. Sequences A007770, A011557, A011557, A031177, A031179, A031180, A031181, A031183, A031184, A031185, A031187, A031188, A031189, A031190, A031191, A031192, A031193, A031194, A031196, A031197, A031198, A031199, A031201, A031202, A031203, A031204, A031205, A031206, A031207, A031208, A031209, A031210, A031357, and A103369 in "The On-Line Encyclopedia of Integer Sequences."
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, p. 28, 2004. https://www.mathematicaguidebooks.org/.



|
|
|
|
كل ما تود معرفته عن أهم فيتامين لسلامة الدماغ والأعصاب
|
|
|
|
|
|
|
ماذا سيحصل للأرض إذا تغير شكل نواتها؟
|
|
|
|
|
|
|
جامعة الكفيل تناقش تحضيراتها لإطلاق مؤتمرها العلمي الدولي السادس
|
|
|