Amicable Triple

Dickson (1913, 2005) defined an amicable triple to be a triple of three numbers 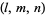 such that

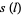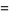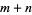			(1)
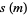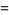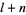			(2)
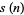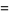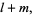			(3)

where 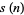 is the restricted divisor function (Madachy 1979). Dickson (1913, 2005) found eight sets of amicable triples with two equal numbers, and two sets with distinct numbers. The latter are (123228768, 103340640, 124015008), for which

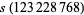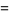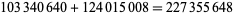			(4)
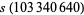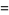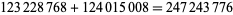			(5)
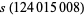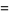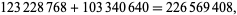			(6)

and (1945330728960, 2324196638720, 2615631953920), for which

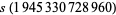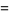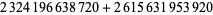			(7)
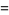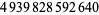			(8)
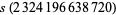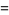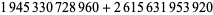			(9)
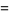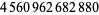			(10)
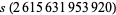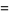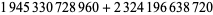			(11)
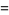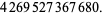			(12)

A second definition (Guy 1994) defines an amicable triple as a triple 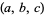 such that

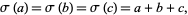(13)

where 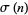 is the divisor function. An example is (, , ).

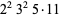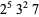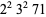REFERENCES:

Borho, W. "Über die Fixpunkte der 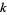-fach iterierten Teilersummenfunktionen." Mitt. Math. Gesellsch. Hamburg 9, 34-48, 1969.

Dickson, L. E. "Amicable Number Triples." Amer. Math. Monthly 20, 84-92, 1913.

Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, p. 50, 2005.

Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 59, 1994.

Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 156, 1979.

Mason, T. E. "On Amicable Numbers and Their Generalizations." Amer. Math. Monthly 28, 195-200, 1921.