Smarandache Sequences

Smarandache sequences are any of a number of simply generated integer sequences resembling those considered in published works by Smarandache such as the consecutive number sequences and Euclid numbers (Iacobescu 1997). Some other "Smarandache" sequences are given below.

1. The concatenation of 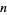 copies of the integer 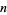: 1, 22, 333, 4444, 55555, ... (OEIS A000461; Marimutha 1997). For 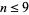, they have the simple formula

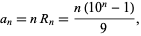(1)

where 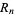 is a repunit. In general,

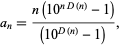(2)

where 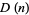 is the number of digits in 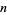. Since the 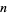th term is always divisible by 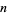, numbers in this sequences can never be prime.

2. The concatenation of the first 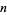 Fibonacci numbers: 1, 11, 112, 1123, 11235, ... (OEIS A019523; Marimutha 1997).

3. The smallest number that is the sum of squares of two distinct earlier terms: 1, 2, 5, 26, 29, 677, ... (OEIS A008318; Bencze 1997).

4. The smallest number that is the sum of squares of any number of distinct earlier terms: 1, 1, 2, 4, 5, 6, 16, 17, ... (OEIS A008319; Bencze 1997).

5. The smallest number that is not the sum of squares of two distinct earlier terms: 1, 2, 3, 4, 6, 7, 8, 9, 11, ... (OEIS A008320; Bencze 1997).

6. The smallest number that is not the sum of squares of any number of distinct earlier terms: 1, 2, 3, 6, 7, 8, 11, ... (OEIS A008321; Bencze 1997).

7. The smallest number that is a sum of cubes of two distinct earlier terms: 1, 2, 9, 730, 737, ... (OEIS A008322; Bencze 1997).

8. The smallest number that is a sum of cubes of any number of distinct earlier terms: 1, 1, 2, 8, 9, 10, 512, 513, 514, ... (OEIS A019511; Bencze 1997).

9. The smallest number that is not a sum of cubes of two distinct earlier terms: 1, 2, 3, 4, 5, 6, 7, 8, 10, ... (OEIS A031980; Bencze 1997).

10. The smallest number that is not a sum of cubes of any number of distinct earlier terms: 1, 2, 3, 4, 5, 6, 7, 10, 11, ... (OEIS A031981; Bencze 1997).

11. The number of partitions of a number 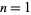, 2, ... into square numbers: 1, 1, 1, 1, 2, 2, 2, 2, 3, 4, 4, 4, 5, 6, 6, 6, 8, 9, 10, 10, 12, 13, ... (OEIS A001156; Iacobescu 1997).

12. The number of partitions of a number 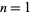, 2, ... into cubic numbers: 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, ... (OEIS A003108; Iacobescu 1997).

13. Two copies of the first 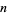 positive integers: 11, 1212, 123123, 12341234, ... (OEIS A019524; Iacobescu 1997).

14. Numbers written in base of triangular numbers: 1, 2, 10, 11, 12, 100, 101, 102, 110, 1000, 1001, 1002, ... (OEIS A000462; Iacobescu 1997).

15. Numbers written in base of double factorial numbers: 1, 10, 100, 101, 110, 200, 201, 1000, 1001, 1010, ... (OEIS A019513; Iacobescu 1997).

16. Sequences starting with terms 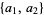 which contain no three-term arithmetic progressions starting with 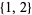: 1, 2, 4, 5, 10, 11, 13, 14, 28, ... (OEIS A003278; Iacobescu 1997, Mudge 1997).

17. Numbers of the form 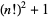: 2, 5, 37, 577, 14401, 518401, 25401601, 1625702401, 131681894401, ... (OEIS A020549; Iacobescu 1997).

18. Numbers of the form 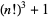: 2, 9, 217, 13825, 1728001, 373248001, 128024064001, ... (OEIS A019514; Iacobescu 1997).

19. Numbers of the form 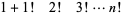: 2, 3, 13, 289, 34561, 24883201, 125411328001, 5056584744960001, ... (OEIS A019515; Iacobescu 1997).

20. Sequences starting with terms 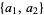 which contain no three-term geometric progressions starting with 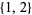: 1, 2, 3, 5, 6, 7, 8, 10, 11, 13, 14, 15, 16, ... (OEIS A000452; Iacobescu 1997).

21. Numbers repeating the digit 1 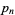 times, where  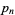is the 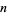th prime: 11, 111, 11111, 1111111, ... (OEIS A031974; Iacobescu 1997). These are a subset of the repunits.

22. Integers with all 2s, 3s, 5s, and 7s (prime digits) removed: 1, 4, 6, 8, 9, 10, 11, 1, 1, 14, 1, 16, 1, 18, 19, 0, ... (OEIS A019516; Iacobescu 1997).

23. Integers with all 0s, 1s, 4s, and 9s (square digits) removed: 2, 3, 5, 6, 7, 8, 2, 3, 5, 6, 7, 8, 2, 2, 22, 23, ... (OEIS A031976; Iacobescu 1997).

24. Smarandache-Fibonacci triples; integers 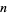 such that 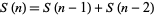, where  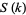is the Smarandache function: 3, 11, 121, 4902, 26245, ... (OEIS A015047; Aschbacher and Mudge 1995; Ibstedt 1997, pp. 19-23; Begay 1997). The largest known is .

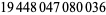25. Smarandache-Radu triplets; integers 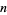 such that there are no primes between the smaller and larger of  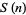and 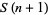: 224, 2057, 265225, ... (OEIS A015048; Radu 1994/1995, Begay 1997, Ibstedt 1997). The largest known is .

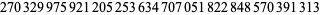26. Smarandache crescendo sequence; integers obtained by concatenating strings of the first 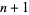 integers for 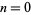, 1, 2, ...: 1, 1, 2, 1, 2, 3, 1, 2, 3, 4, ... (OEIS A002260; Brown 1997, Brown and Castillo 1997). The 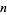th term is given by 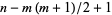, where 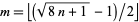, with  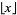the floor function (Hamel 1997).

27. Smarandache descrescendo sequence; integers obtained by concatenating strings of the first 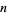 integers for 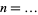, 2, 1: 1, 2, 1, 3, 2, 1, 4, 3, 2, 1, ... (OEIS A004736; Smarandache 1997, Brown 1997).

28. Smarandache crescendo pyramidal sequence, a.k.a. Smarandache descrescendo symmetric sequence; integers obtained by concatenating strings of rising and falling integers: 1, 1, 2, 1, 1, 2, 3, 2, 1, 1, 2, 3, 4, 3, 2, 1, ... (OEIS A004737; Brown 1997, Brown and Castillo 1997, Smarandache 1997).

29. Smarandache descrescendo pyramidal sequence; integers obtained by concatenating strings of falling and rising integers: 1, 2, 1, 2, 3, 2, 1, 2, 3, 4, 3, 2, 1, 2, 3, 4, ... (OEIS A004738; Brown 1997).

30. Smarandache crescendo symmetric sequence: 1, 1, 1, 2, 2, 1, 1, 2, 3, 3, 2, 1, ... (OEIS A004739; Brown 1997, Smarandache 1997).

31. Smarandache permutation sequence; numbers obtained by concatenating sequences of increasing length of increasing odd numbers and decreasing even numbers: 1, 2, 1, 3, 4, 2, 1, 3, 5, 6, 4, 2, ... (OEIS A004741; Brown 1997, Brown and Castillo 1997).

32. Smarandache pierced chain sequence; numbers of the form 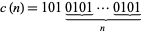 for 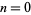, 1, ...: 101, 1010101, 10101010101, ... (OEIS A031982; Ashbacher 1997). In addition,  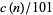contains no primes (Ashbacher 1997).

33. Smarandache symmetric sequence: 1, 11, 121, 1221, 12321, 123321, ... (OEIS A007907; Smarandache 1993, Dumitrescu and Seleacu 1994, sequence 3; Mudge 1995).

34. Smarandache square-digital sequence; square numbers all of whose digits are also squares: 1, 4, 9, 49, 100, 144, ... (OEIS A019544; Mudge 1997).

35. Square-digits; numbers composed of digits which are squares: 0, 1, 4, 9, 10, 11, 14, 19, 40, 41, ... (OEIS A046030).

36. Cube-digits; numbers composed of digits which are cubes: 1, 8, 10, 11, 18, 80, 81, 88, 100, 101, ... (OEIS A046031).

37. Smarandache cube-digital sequence; cube-digit numbers which are themselves cubes: 1, 8, 1000, 8000, 1000000, ... (OEIS A019545; Mudge 1997).

38. Prime-digits; numbers composed of digits which are primes: 2, 3, 5, 7, 22, 23, 25, 27, 32, 33, 35, ... (OEIS A046034).

39. Smarandache prime-digital sequence; prime-digit numbers which are themselves prime: 2, 3, 5, 7, 23, 37, 53, ... (OEIS A019546; Smith 1996, Mudge 1997). Dubner (2002) found the largest-known members of this sequence,

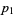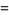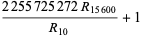			(3)
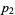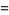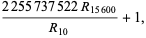			(4)

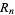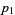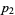where  is a repunit and both  and  have 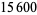 digits.

40. Smarandache deconstructive sequence; integers constructed by sequentially repeating the digits 1-9 in the following way: 1, 23, 456, 7891, 23456, 789123, 4567891, ... (OEIS A007923; Smarandache 1993, Kashihara 1996, Ashbacher 1998, Atanassov 1999ab). Of these, 23, 4567891, 23456789, 1234567891, ... (OEIS A050234) are prime (Kashihara 1996, Ashbacher 1998).

REFERENCES:

Ashbacher, C. Collection of Problems on Smarandache Notions. Vail, AZ: Erhus University Press, 1996.

Ashbacher, C. "Problem 4616." School Sci. Math. 97, 221, 1997.

Ashbacher, C. Pluckings from the Tree of Smarandache Sequences and Functions. Lupton, AZ: American Research Press, 1998.

Ashbacher, C. "Some Problems Concerning the Smarandache Deconstructive Sequence." J. Recr. Math. 29, 82-84, 1998.

Aschbacher, C. and Mudge, M. Personal Computer World. p. 302, Oct. 1995.

Atanassov, K. "On the 4th Smarandache Problem." Notes on Number Theory and Discrete Mathematics (Sophia, Bulgaria) 5, 33-35, 1999a.

Atanassov, K. T. On Some of the Smarandache's Problems. Lupton, AZ: American Research Press, pp. 16-21, 1999b.

Begay, A. "Smarandache Ceil Functions." Bull. Pure Appl. Sci. 16E, 227-229, 1997.

Bencze, M. "Smarandache Recurrence Type Sequences." Bull. Pure Appl. Sci. 16E, 231-236, 1997.

Bencze, M. and Tutescu, L. (Eds.). Some Notions and Questions in Number Theory, Vol. 2. https://www.gallup.unm.edu/~smarandache/SNAQINT2.TXT.

Brown, J. "Crescendo & Descrescendo." In Richard Henry Wilde: An Anthology in Memoriam (1789-1847) (Ed. M. Myers). Bristol, IN: Bristol Banner Books, p. 19, 1997.

Brown, J. and Castillo, J. "Problem 4619." School Sci. Math. 97, 221-222, 1997.

Dubner, H. "Fw: [PrimeNumbers] Record Primes with All Prime Digits." 17 Feb 2002. https://listserv.nodak.edu/scripts/wa.exe?A2=ind0202&L=nmbrthry&P=1697.

Dumitrescu, C. and Seleacu, V. (Eds.). Some Notions and Questions in Number Theory, 4th ed. Glendale, AZ: Erhus University Press, 1994. https://www.gallup.unm.edu/~smarandache/SNAQINT.TXT.

Dumitrescu, C. and Seleacu, V. (Eds.). Proceedings of the First International Conference on Smarandache Type Notions in Number Theory. Lupton, AZ: American Research Press, 1997.

Hamel, E. Solution to Problem 4619. School Sci. Math. 97, 221-222, 1997.

Iacobescu, F. "Smarandache Partition Type and Other Sequences." Bull. Pure Appl. Sci. 16E, 237-240, 1997.

Ibstedt, H. Surfing on the Ocean of Numbers--A Few Smarandache Notions and Similar Topics. Lupton, AZ: Erhus University Press, 1997.

Kashihara, K. Comments and Topics on Smarandache Notions and Problems. Vail, AZ: Erhus University Press, 1996.

Marimutha, H. "Smarandache Concatenate Type Sequences." Bull. Pure Appl. Sci. 16E, 225-226, 1997.

Mudge, M. "Top of the Class." Personal Computer World, 674-675, June 1995.

Mudge, M. "Not Numerology but Numeralogy!" Personal Computer World, 279-280, 1997.

Programs and the Abstracts of the First International Conference on Smarandache Notions in Number Theory. Craiova, Romania, Aug. 21-23, 1997.

Radu, I. M. Mathematical Spectrum 27, 43, 1994/1995.

Rivera, C. "Problems & Puzzles: Puzzle 008-Primes by Listing." https://www.primepuzzles.net/puzzles/puzz_008.htm.

Sloane, N. J. A. Sequences A000452, A000461, A000462, A001156/M0221, A002260, A003108/M0209, A003278/M0975, A004736, A004737, A004738, A004739, A004741, A007907, A007923, A008318, A008319, A008320, A008321, A008322, A015047, A015048, A019524, A019511, A019513, A019514, A019515, A019516, A019523, A019544, A019545, A019546 A020549, A031974, A031976, A031980, A031981, A031982, A046030, A046031, A046034, and A050234 in "The On-Line Encyclopedia of Integer Sequences."

Smarandache, F. "Properties of the Numbers." Tempe, AZ: Arizona State University Special Collection, 1975.

Smarandache, F. Only Problems, Not Solutions! 4th ed. Phoenix, AZ: Xiquan, 1993.

Smarandache, F. Collected Papers, Vol. 2. Kishinev, Moldova: Kishinev University Press, 1997.

Smith, S. "A Set of Conjectures on Smarandache Sequences." Bull. Pure Appl. Sci. 15E, 101-107, 1996.