Elliptic Curve Primality Proving

Elliptic curve primality proving, abbreviated ECPP, is class of algorithms that provide certificates of primality using sophisticated results from the theory of elliptic curves. A detailed description and list of references are given by Atkin and Morain (1990, 1993).

Adleman and Huang (1987) designed an independent algorithm using hyperelliptic curves of genus two.

ECPP is the fastest known general-purpose primality testing algorithm. ECPP has a running time of 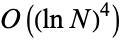. As of 2004, the program PRIMO can certify a 4769-digit prime in approximately 2000 hours of computation (or nearly three months of uninterrupted computation) on a 1 GHz processor using this technique. As of 2009, the largest prime certified using this technique was the 11th Mills' prime (https://primes.utm.edu/primes/page.php?id=77907)

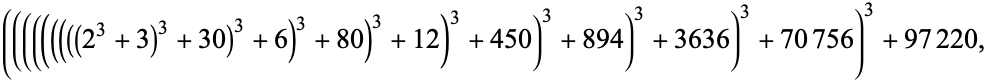which has 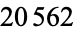 decimal digits. The proof was performed using a distributed computation that started in September 2005 and ended in June 2006 and required a cumulative CPU-time corresponding to 2.39 GHz for 2219 days (just over 6 years).

REFERENCES:

Adleman, L. M. and Huang, M. A. "Recognizing Primes in Random Polynomial Time." In Proc. 19th STOC, New York City, May 25-27, 1986. New York: ACM Press, pp. 462-469, 1987.

Alpern, D. "Factorization Using the Elliptic Curve Method." https://www.alpertron.com.ar/ECM.HTM.

Atkin, A. O. L. Lecture notes of a conference, Boulder, CO, Aug. 1986.

Atkin, A. O. L. and Morain, F. "Elliptic Curves and Primality Proving." Res. Rep. 1256, INRIA, June 1990.

Atkin, A. O. L. and Morain, F. "Elliptic Curves and Primality Proving." Math. Comput. 61, 29-68, 1993.

Bosma, W. "Primality Testing Using Elliptic Curves." Techn. Rep. 85-12, Math. Inst., Univ. Amsterdam, 1985.

Chudnovsky, D. V. and Chudnovsky, G. V. "Sequences of Numbers Generated by Addition in Formal Groups and New Primality and Factorization Tests." Res. Rep. RC 11262, IBM, Yorktown Heights, NY, 1985.

Cohen, H. Cryptographie, factorisation et primalité: l'utilisation des courbes elliptiques. Paris: C. R. J. Soc. Math. France, Jan. 1987.

Kaltofen, E.; Valente, R.; and Yui, N. "An Improved Las Vegas Primality Test." Res. Rep. 89-12, Rensselaer Polytechnic Inst., Troy, NY, May 1989.

Martin, M. "PRIMO--Primality Proving." https://www.ellipsa.net.

Martin, M. "20 Greatest Candidates Verified with Primo." https://www.ellipsa.net/primo/top20.html.