Adleman-Pomerance-Rumely Primality Test

A modified Miller's primality test which gives a guarantee of primality or compositeness. The algorithm's running time for a number 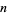 has been proved to be as  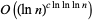for some 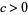. It was simplified by Cohen and Lenstra (1984), implemented by Cohen and Lenstra (1987), and subsequently optimized by Bosma and van der Hulst (1990).

REFERENCES:

Adleman, L. M.; Pomerance, C.; and Rumely, R. S. "On Distinguishing Prime Numbers from Composite Number." Ann. Math. 117, 173-206, 1983.

Bosma, W. and van der Hulst, M.-P. "Faster Primality Testing." In Advances in Cryptology, Proc. Eurocrypt '89, Houthalen, April 10-13, 1989 (Ed. J.-J. Quisquater). New York: Springer-Verlag, 652-656, 1990.

Brillhart, J.; Lehmer, D. H.; Selfridge, J.; Wagstaff, S. S. Jr.; and Tuckerman, B. Factorizations of b-n+/-1, b=2, 3, 5, 6, 7, 10, 11, 12 Up to High Powers, rev. ed. Providence, RI: Amer. Math. Soc., pp. lxxxiv-lxxxv, 1988.

Cohen, H. and Lenstra, A. K. "Primality Testing and Jacobi Sums." Math. Comput. 42, 297-330, 1984.

Cohen, H. and Lenstra, A. K. "Implementation of a New Primality Test." Math. Comput. 48, 103-121, 1987.

Mihailescu, P. "A Primality Test Using Cyclotomic Extensions." In Applied Algebra, Algebraic Algorithms and Error-Correcting Codes: Proceedings of the Sixth International Conference (AAECC-6) held in Rome, July 4-8, 1988 (Ed. T. Mora). New York: Springer-Verlag, pp. 310-323, 1989.