Wilson Prime 

A Wilson prime is a prime satisfying

where 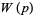 is the Wilson quotient, or equivalently,

The first few Wilson primes are 5, 13, and 563 (OEIS A007540). Crandall et al. (1997) showed there are no others less than  (McIntosh 2004), a limit that has subsequently been increased to  (Costa et al. 2012).

REFERENCES:

Costa, E.; Gerbicz, R.; and Harvey, D. "A Search for Wilson Primes." 5 Dec 2012. https://arxiv.org/abs/1209.3436.

Crandall, R.; Dilcher, K; and Pomerance, C. "A search for Wieferich and Wilson Primes." Math. Comput. 66, 433-449, 1997.

Gonter, R. H. and Kundert, E. G. "All Numbers Up to  Have Been Tested without Finding a New Wilson Prime." Preprint, 1994.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 167, 2003.

McIntosh, R. email to Paul Zimmermann. 9 Mar 2004. https://www.loria.fr/~zimmerma/records/Wieferich.status.

Mersenne Forum. "Wilson-Prime Search Practicalities." https://www.mersenneforum.org/showthread.php?t=16028.

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 56, 1983.

Ribenboim, P. "Wilson Primes." §5.4 in The New Book of Prime Number Records. New York: Springer-Verlag, pp. 346-350, 1996.

Sloane, N. J. A. Sequence A007540/M3838 in "The On-Line Encyclopedia of Integer Sequences."

Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 73, 1991.