


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-5-2020
Date: 21-9-2020
Date: 19-3-2020
|
A Gaussian sum is a sum of the form
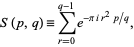 |
(1) |
where 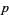 and
and 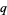 are relatively prime integers. The symbol
are relatively prime integers. The symbol 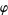 is sometimes used instead of
is sometimes used instead of 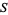 . Although the restriction to relatively prime integers is often useful, it is not necessary, and Gaussian sums can be written so as to be valid for all integer
. Although the restriction to relatively prime integers is often useful, it is not necessary, and Gaussian sums can be written so as to be valid for all integer 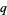 (Borwein and Borwein 1987, pp. 83 and 86).
(Borwein and Borwein 1987, pp. 83 and 86).
If 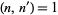 , then
, then
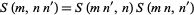 |
(2) |
(Nagell 1951, p. 178). Gauss showed that
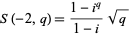 |
(3) |
for odd 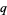 . Written explicitly
. Written explicitly
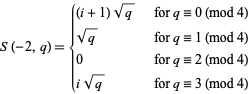 |
(4) |
(Nagell 1951, p. 177).
For 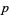 and
and 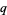 of opposite parity (i.e., one is even and the other is odd), Schaar's identity states
of opposite parity (i.e., one is even and the other is odd), Schaar's identity states
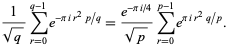 |
(5) |
Such sums are important in the theory of quadratic residues.
REFERENCES:
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity. New York: Wiley, 1987.
Evans, R. and Berndt, B. "The Determination of Gauss Sums." Bull. Amer. Math. Soc. 5, 107-129, 1981.
Katz, N. M. Gauss Sums, Kloosterman Sums, and Monodromy Groups. Princeton, NJ: Princeton University Press, 1987.
Malyšev, A. V. "Gauss and Kloosterman Sums." Dokl. Akad. Nauk SSSR 133, 1017-1020, 1960. English translation in Soviet Math. Dokl. 1, 928-932, 1960.
Nagell, T. "The Gaussian Sums." §53 in Introduction to Number Theory. New York: Wiley, pp. 177-180, 1951.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 132-134, 1994.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|