المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Ramanujan,s Sum Identity |
 486
 04:10 مساءً
date: 18-7-2020 |
Author : Hirschhorn, M. D. 
Book or Source : "An Amazing Identity of Ramanujan." Math. Mag. 68 
Page and Part : ...|
Read More
Date: 27-1-2020
592
Date: 13-12-2020
969
Date: 10-4-2020
757
|
Given the generating functions defined by
 |
 |
 |
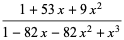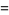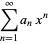(1) |
 |
 |
 |
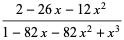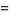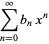(2) |
 |
 |
 |
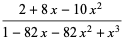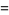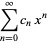(3) |
(OEIS A051028, A051029, and A051030), then
 |
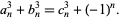(4) |
Hirschhorn (1995) showed that
 |
 |
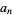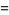![1/(85)[(64+8sqrt(85))alpha^n+(64-8sqrt(85))beta^n-43(-1)^n]](https://mathworld.wolfram.com/images/equations/RamanujansSumIdentity/Inline12.gif) |
(5) |
 |
 |
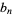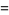![1/(85)[(77+7sqrt(85))alpha^n+(77-7sqrt(85))beta^n+16(-1)^n]](https://mathworld.wolfram.com/images/equations/RamanujansSumIdentity/Inline15.gif) |
(6) |
 |
 |
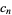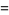![1/(85)[(93+9sqrt(85))alpha^n+(93-9sqrt(85))beta^n-16(-1)^n],](https://mathworld.wolfram.com/images/equations/RamanujansSumIdentity/Inline18.gif) |
(7) |
where
 |
 |
 |
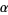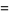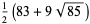(8) |
 |
 |
 |
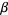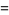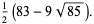(9) |
Hirschhorn (1996) showed that checking the first seven cases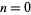 
to 6 is sufficient to prove the result.
REFERENCES:
Hirschhorn, M. D. "An Amazing Identity of Ramanujan." Math. Mag. 68, 199-201, 1995.
Hirschhorn, M. D. "A Proof in the Spirit of Zeilberger of an Amazing Identity of Ramanujan." Math. Mag. 69, 267-269, 1996.
Sloane, N. J. A. Sequences A051028, A051029, and A051030 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|
