Diophantine Equation--10th Powers
المؤلف:
Ekl, R. L.
المصدر:
"New Results in Equal Sums of Like Powers." Math. Comput. 67
الجزء والصفحة:
...
22-5-2020
1023
Diophantine Equation--10th Powers
The 10.1.2 equation
 |
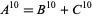(1)
|
is a special case of Fermat's last theorem with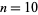 
, and so has no solution. No 
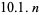solutions are known with 
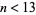. A 10.1.13 solution is
 |
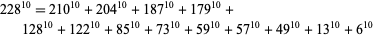(2)
|
(S. Chase). The smallest 10.1.15 solution is
 |
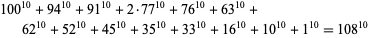(3)
|
(J.-C. Meyrignac 1999). The smallest 10.1.22 solution is
 |
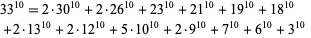(4)
|
(Ekl 1998). The smallest 10.1.23 solution is
 |
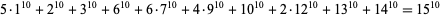(5)
|
(Lander et al. 1967).
10.2.12 solutions include
 |
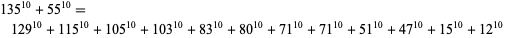(6)
|
 |
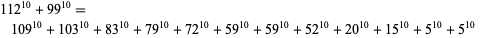(7)
|
(V. Pliousnine 2000, N. Kuosa 2000). The smallest 10.2.13 solution is
 |
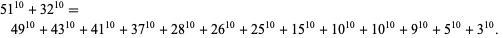(8)
|
The smallest 10.2.15 solution is
 |
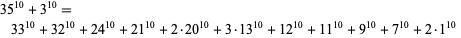(9)
|
(Ekl 1998). The smallest 10.2.19 solution is
 |
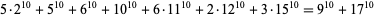(10)
|
(Lander et al. 1967). A 10.3.11 solution is
 |
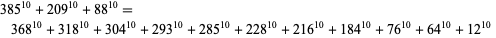(11)
|
(J. Wroblewski 2002). A 10.3.12 solution is
 |
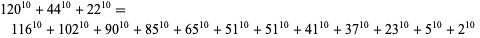(12)
|
(T. Nolan 2000). The smallest 10.3.13 solution is
 |
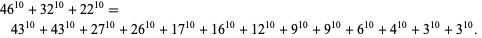(13)
|
The smallest 10.3.14 solution is
 |
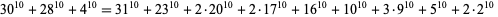(14)
|
(Ekl 1998). The smallest 10.3.24 solution is
 |
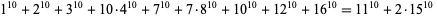(15)
|
(Lander et al. 1967).
A 10.4.9 solution is
 |
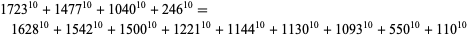(16)
|
(J. Wroblewski 2002). 10.4.10 solutions include
 |
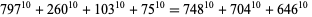(17)
|
 |
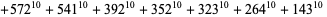(18)
|
 |
(19)
|
 |
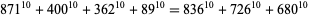(20)
|
 |
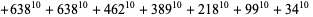(21)
|
 |
(22)
|
 |
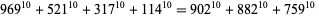(23)
|
 |
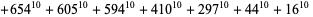(24)
|
 |
(25)
|
 |
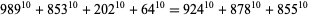(26)
|
 |
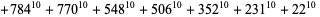(27)
|
 |
(28)
|
 |
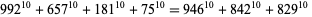(29)
|
 |
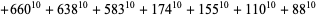(30)
|
 |
(31)
|
 |
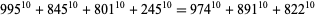(32)
|
 |
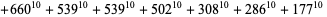(33)
|
 |
(34)
|
 |
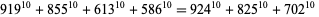(35)
|
 |
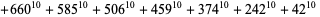(36)
|
 |
(37)
|
 |
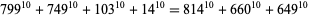(38)
|
 |
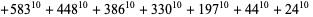(39)
|
 |
(40)
|
 |
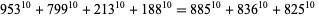(41)
|
 |
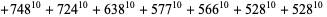(42)
|
 |
(43)
|
 |
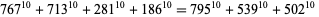(44)
|
 |
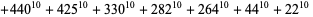(45)
|
 |
(46)
|
 |
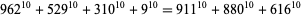(47)
|
 |
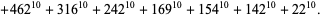(48)
|
(J. Wroblewski 2002). A 10.4.11 solution is
 |
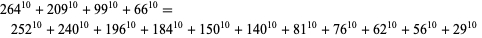(49)
|
(S. Chase). The 10.4.12 equation has solution
 |
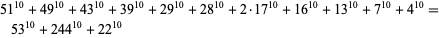(50)
|
(E. Bainville 1999). The smallest 10.4.15 solution is
 |
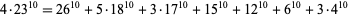(51)
|
(Ekl 1998). The smallest 10.4.23 solution is
 |
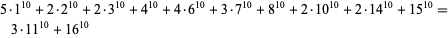(52)
|
(Lander et al. 1967).
The smallest 10.5.16 solutions are
 |
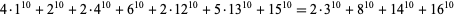(53)
|
 |
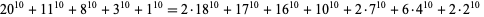(54)
|
(Lander et al. 1967, Ekl 1998).
The smallest 10.6.6 solution is
 |
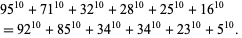(55)
|
The smallest 10.6.16 solution is
 |
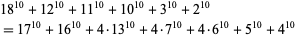(56)
|
(Ekl 1998). The smallest 10.6.27 solution is
 |
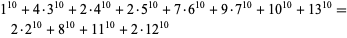(57)
|
(Lander et al. 1967).
The smallest 10.7.7 solutions are
(Lander et al. 1967, Ekl 1998).
REFERENCES:
Ekl, R. L. "New Results in Equal Sums of Like Powers." Math. Comput. 67, 1309-1315, 1998.
Lander, L. J.; Parkin, T. R.; and Selfridge, J. L. "A Survey of Equal Sums of Like Powers." Math. Comput. 21, 446-459, 1967.
Meyrignac, J.-C. "Computing Minimal Equal Sums of Like Powers." https://euler.free.fr.
الاكثر قراءة في نظرية الاعداد
اخر الاخبار
اخبار العتبة العباسية المقدسة
