


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-8-2020
Date: 16-11-2020
Date: 5-8-2020
|
A classic arithmetical problem probably first posed by Euclid and investigated by various authors in the Middle Ages.
The problem is formulated as a dialogue between the two animals after which it is called. The mule say to the ass, "If you gave me one of your sacks, I would have as many as you." The ass replies, "If you gave one of your sacks, I would have twice as many as you." The question, of course, is "How many sacks do they have?" The number  of sacks of the mule and the number
of sacks of the mule and the number 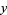 of sacks of the ass are related by the identities:
of sacks of the ass are related by the identities:
 |
 |
 |
(1) |
 |
 |
 |
(2) |
which form a system of two linear equations. The solution is 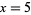 ,
, 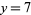 .
.
A generalization of this problem has been studied by Singmaster (1999, 2002). In this modified problem, the ass says, "If you gave me 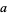 of your sacks, I would have
of your sacks, I would have 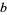 times as many as you," and the mule answers, "If you gave my
times as many as you," and the mule answers, "If you gave my 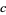 of your sacks, I would have
of your sacks, I would have 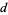 times as many as you." This has solutions
times as many as you." This has solutions
 |
 |
 |
(3) |
 |
 |
 |
(4) |
which are integers only when 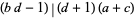 and
and 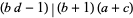 .
.
REFERENCES:
Singmaster, D. "Some Diophantine Recreations." In The Mathemagician and the Pied Puzzler: A Collection in Tribute to Martin Gardner (Ed. E. Berlekamp and T. Rodgers). Boston, MA: A K Peters, pp. 219-235, 1999.
Singmaster, D. "A Variation of the Ass and Mule Problem." Crux Math. 28, 236-238, 2002.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|