
 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 31-1-2020
Date: 14-9-2020
Date: 8-10-2020
|
There are a number of functions in various branches of mathematics known as Riemann functions. Examples include the Riemann P-series, Riemann-Siegel functions, Riemann theta function, Riemann zeta function, xi-function, the function 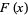 obtained by Riemann in studying Fourier series, the function
obtained by Riemann in studying Fourier series, the function 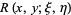 appearing in the application of the Riemann method for solving the Goursat problem, the Riemann prime counting function
appearing in the application of the Riemann method for solving the Goursat problem, the Riemann prime counting function 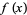 , and the related the function
, and the related the function 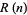 obtained by replacing
obtained by replacing 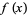 with
with 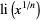 in the Möbius inversion formula.
in the Möbius inversion formula.
The Riemann function 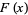 for a Fourier series
for a Fourier series
![1/2a_0+sum_(n=1)^infty[a_ncos(nx)+b_nsin(nx)]](https://mathworld.wolfram.com/images/equations/RiemannFunction/NumberedEquation1.gif) |
(1) |
is obtained by integrating twice term by term to obtain
![F(x)=1/4a_0x^2-sum_(n=1)^infty1/(n^2)[a_ncos(nx)+b_nsin(nx)]+Cx+D,](https://mathworld.wolfram.com/images/equations/RiemannFunction/NumberedEquation2.gif) |
(2) |
where 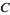 and
and 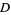 are constants (Riemann 1957; Hazewinkel 1988, vol. 8, p. 118).
are constants (Riemann 1957; Hazewinkel 1988, vol. 8, p. 118).
The Riemann function 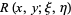 arises in the solution of the linear case of the Goursat problem of solving the hyperbolic partial differential equation
arises in the solution of the linear case of the Goursat problem of solving the hyperbolic partial differential equation
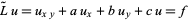 |
(3) |
with boundary conditions
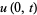 |
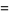 |
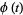 |
(4) |
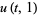 |
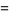 |
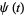 |
(5) |
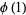 |
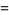 |
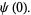 |
(6) |
Here, 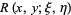 is defined as the solution of the equation
is defined as the solution of the equation
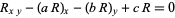 |
(7) |
which satisfies the conditions
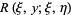 |
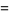 |
![exp[int_eta^ya(xi,t)dt]](https://mathworld.wolfram.com/images/equations/RiemannFunction/Inline23.gif) |
(8) |
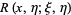 |
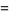 |
![exp[int_xi^xb(t,eta)dt]](https://mathworld.wolfram.com/images/equations/RiemannFunction/Inline26.gif) |
(9) |
on the characteristics 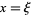 and
and 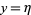 , where
, where 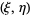 is a point on the domain
is a point on the domain 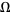 on which (8) is defined (Hazewinkel 1988). The solution is then given by the Riemann formula
on which (8) is defined (Hazewinkel 1988). The solution is then given by the Riemann formula
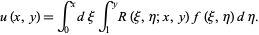 |
(10) |
This method of solution is called the Riemann method.
REFERENCES:
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 144-145, 1996.
Hazewinkel, M. (Managing Ed.). Encyclopaedia of Mathematics: An Updated and Annotated Translation of the Soviet "Mathematical Encyclopaedia." Dordrecht, Netherlands: Reidel, Vol. 4, p. 289 and Vol. 8, p. 125, 1988.
Knuth, D. E. The Art of Computer Programming, Vol. 2: Seminumerical Algorithms, 3rd ed. Reading, MA: Addison-Wesley, 1998.
Riemann, B. "Über die Darstellbarkeit einer Function durch eine trigonometrische Reihe." Reprinted in Gesammelte math. Abhandlungen. New York: Dover, pp. 227-264, 1957.



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
لتعزيز التواصل مع الزائرات الأجنبيات : العتبة العلويّة المقدّسة تُطلق دورة لتعليم اللغة الإنجليزية لخادمات القسم النسويّ
|
|
|