


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-12-2019
Date: 4-1-2021
Date: 29-8-2020
|
Convergents of the pi continued fractions are the simplest approximants to 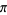 . The first few are given by 3, 22/7, 333/106, 355/113, 103993/33102, 104348/33215, ... (OEIS A002485 and A002486), which are good to 0, 2, 4, 6, 9, 9, 9, 10, 11, 11, 12, 13, ... (OEIS A114526) decimal digits, respectively.
. The first few are given by 3, 22/7, 333/106, 355/113, 103993/33102, 104348/33215, ... (OEIS A002485 and A002486), which are good to 0, 2, 4, 6, 9, 9, 9, 10, 11, 11, 12, 13, ... (OEIS A114526) decimal digits, respectively.
Two approximations follow from the near-identity function 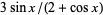 evaluated at
evaluated at 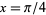 and
and 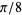 , giving
, giving
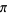 |
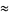 |
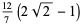 |
(1) |
 |
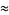 |
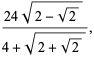 |
(2) |
which are good to 2 and 3 digits, respectively.
Kochanski's approximation is the root of
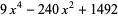 |
(3) |
given by
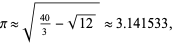 |
(4) |
which is good to 4 digits.
Another curious fact is the almost integer
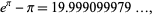 |
(5) |
which can also be written as
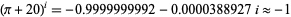 |
(6) |
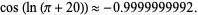 |
(7) |
Here, 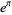 is Gelfond's constant. Applying cosine a few more times gives
is Gelfond's constant. Applying cosine a few more times gives
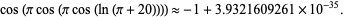 |
(8) |
Another approximation involving 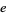 is given by
is given by
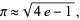 |
(9) |
which is good to 2 decimal digits (A. Povolotsky, pers. comm., Mar. 6, 2008).
An apparently interesting near-identity is given by
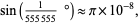 |
(10) |
which becomes less surprising when it is noted that 555555 is a repdigit, so the above is just a special case of the near-identity
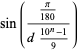 |
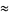 |
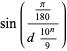 |
(11) |
 |
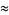 |
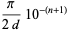 |
(12) |
with 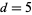 and
and 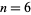 .
.
An approximation involving the golden ratio 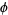 is
is
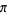 |
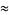 |
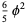 |
(13) |
 |
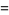 |
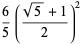 |
(14) |
 |
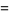 |
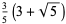 |
(15) |
 |
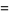 |
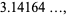 |
(16) |
which is good to 4 digits. A similar approximation due to S. Mircea-Mugurel (pers. comm., Oct. 30, 2002) is given by
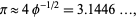 |
(17) |
which however is only good to two decimal places. Another approximation involving the golden ratio 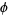 is given by
is given by
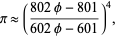 |
(18) |
which is good to 7 digits (K. Rashid, pers. comm.).
Some approximations due to Ramanujan include
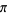 |
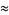 |
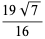 |
(19) |
 |
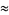 |
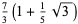 |
(20) |
 |
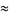 |
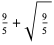 |
(21) |
 |
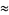 |
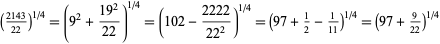 |
(22) |
 |
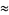 |
 |
(23) |
 |
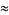 |
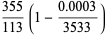 |
(24) |
 |
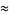 |
![(12)/(sqrt(130))ln[((3+sqrt(13))(sqrt(8)+sqrt(10)))/2]](https://mathworld.wolfram.com/images/equations/PiApproximations/Inline55.gif) |
(25) |
 |
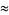 |
![(24)/(sqrt(142))ln[(sqrt(10+11sqrt(2))+sqrt(10+7sqrt(2)))/2]](https://mathworld.wolfram.com/images/equations/PiApproximations/Inline58.gif) |
(26) |
 |
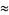 |
![(12)/(sqrt(190))ln[(3+sqrt(10))(sqrt(8)+sqrt(10))]](https://mathworld.wolfram.com/images/equations/PiApproximations/Inline61.gif) |
(27) |
 |
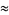 |
![(12)/(sqrt(310))ln[1/4(3+sqrt(5))(2+sqrt(2))(5+2sqrt(10)+sqrt(61+20sqrt(10)))]](https://mathworld.wolfram.com/images/equations/PiApproximations/Inline64.gif) |
(28) |
 |
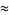 |
![4/(sqrt(522))ln[((5+sqrt(29))/(sqrt(2)))^3(5sqrt(29)+11sqrt(6))(sqrt((9+3sqrt(6))/4)+sqrt((5+3sqrt(6))/4))^6],](https://mathworld.wolfram.com/images/equations/PiApproximations/Inline67.gif) |
(29) |
which are accurate to 3, 4, 4, 8, 8, 9, 14, 15, 15, 18, 23, 31 digits, respectively (Ramanujan 1913-1914; Hardy 1952, p. 70; Wells 1986, p. 54; Berndt 1994, pp. 48-49 and 88-89). Equation (◇) and the similar
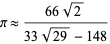 |
(30) |
are also given by Borwein and Bailey (2003, p. 135). Ramanujan also gave
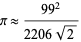 |
(31) |
(Wells 1986, p. 54).
S. Irvine (pers. comm.) noted that (◇), giving an approximation to 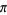 good to 8 digits, can be written in a pandigital form (i.e., using all digits 0-9 exactly once) as
good to 8 digits, can be written in a pandigital form (i.e., using all digits 0-9 exactly once) as
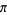 |
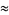 |
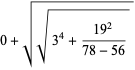 |
(32) |
 |
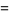 |
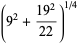 |
(33) |
 |
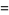 |
 |
(34) |
(S. Plouffe, pers. comm.; cf. Wells 1986, p. 54). E. Pegg (pers. comm.) found the pandigital approximation
 |
(35) |
which approximates 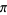 to 9 digits. Another pandigital formula is given by
to 9 digits. Another pandigital formula is given by
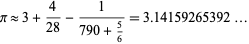 |
(36) |
(B. Astle, pers. comm., Jan. 9, 2004), which approximates 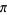 to 9 digits. Surpassing both of these is the pandigital approximation
to 9 digits. Surpassing both of these is the pandigital approximation
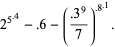 |
(37) |
which gives 10 correct digits (B. Ziv, pers. comm., Jul. 7, 2004). A further pandigital approximation is given by
![(ln{[2×5!+(8-1)!]^(sqrt(9))+4!+(3!)!})/(sqrt(67)),](https://mathworld.wolfram.com/images/equations/PiApproximations/NumberedEquation16.gif) |
(38) |
which is good to 17 digits (G. W. Barbosa, pers. comm.).
M. Schneider (pers. comm., May 6, 2008) found the approximation
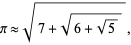 |
(39) |
which is good to 3 decimal digits. P. Lindborg (pers. comm.) noted that the convergent 104348/33125 can be written in the slightly curious form
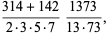 |
(40) |
which is good to 9 digits.
Other approximations due to E. Pegg include
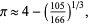 |
(41) |
which is good to 6 digits (pers. comm., March 2, 2002) and
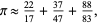 |
(42) |
which is good to 9 digits (pers. comm., Dec. 30, 2002).
A simple approximation involving the cube root is
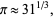 |
(43) |
which is good to 3 digits (M. Joseph, pers. comm., May 3, 2006). A more exotic one is given by
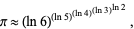 |
(44) |
which is good to 4 digits (M. Joseph, pers. comm., May 3, 2006).
Castellanos (1988ab) gives a slew of curious formulas:
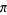 |
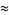 |
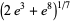 |
(45) |
 |
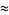 |
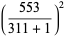 |
(46) |
 |
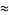 |
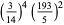 |
(47) |
 |
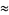 |
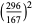 |
(48) |
 |
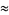 |
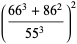 |
(49) |
 |
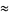 |
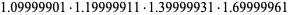 |
(50) |
 |
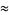 |
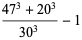 |
(51) |
 |
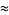 |
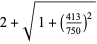 |
(52) |
 |
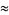 |
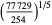 |
(53) |
 |
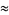 |
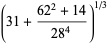 |
(54) |
 |
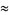 |
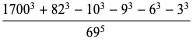 |
(55) |
 |
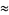 |
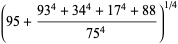 |
(56) |
 |
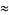 |
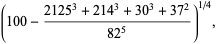 |
(57) |
which are accurate to 3, 4, 4, 5, 6, 7, 7, 8, 9, 10, 11, 12, and 13 digits, respectively. An extremely accurate approximation due to Shanks (1982) is
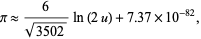 |
(58) |
where 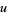 is the product of four simple quartic units.
is the product of four simple quartic units.
David W. Hoffman (pers. comm.) gave
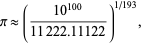 |
(59) |
where the numerator is one googol, which is good to 9 digits. The approximations
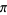 |
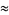 |
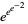 |
(60) |
 |
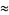 |
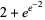 |
(61) |
give 2 digits (G. von Hippel, pers. comm.).
A sequence of approximations due to Plouffe and Borwein and Bailey (2003, pp. 115 and 134-135) includes
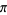 |
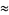 |
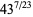 |
(62) |
 |
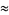 |
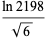 |
(63) |
 |
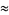 |
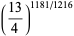 |
(64) |
 |
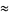 |
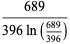 |
(65) |
 |
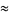 |
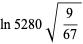 |
(66) |
 |
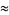 |
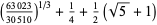 |
(67) |
 |
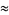 |
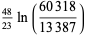 |
(68) |
 |
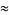 |
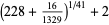 |
(69) |
 |
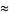 |
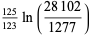 |
(70) |
 |
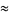 |
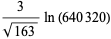 |
(71) |
 |
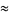 |
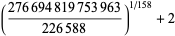 |
(72) |
 |
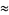 |
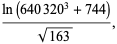 |
(73) |
which are accurate to 4, 5, 7, 7, 9, 10, 11, 11, 11, 15, 23, and 30 digits, respectively.
The last expression, which follows from the series expansion of the j-function. Carrying this one step further gives
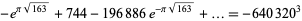 |
(74) |
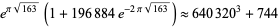 |
(75) |
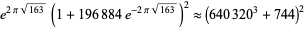 |
(76) |
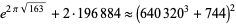 |
(77) |
giving
![pi approx (ln[(640320^3+744)^2-2·196884])/(2sqrt(163)),](https://mathworld.wolfram.com/images/equations/PiApproximations/NumberedEquation29.gif) |
(78) |
which is good to 46 decimal digits (Warda, pers. comm., Nov. 15, 2004).
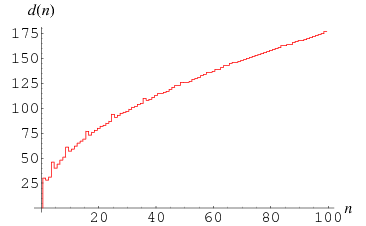
Interestingly, 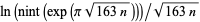 gives successively good approximations to
gives successively good approximations to 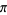 for larger and larger
for larger and larger 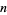 (Warda, pers. comm., Nov. 22, 2004). In particular, the number of correct digits for
(Warda, pers. comm., Nov. 22, 2004). In particular, the number of correct digits for 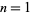 , 2, ... are given by 30, 28, 31, 46, 40, 44, 48, 51, 61, 57, 59, 62, 65 (OEIS A100935).
, 2, ... are given by 30, 28, 31, 46, 40, 44, 48, 51, 61, 57, 59, 62, 65 (OEIS A100935).
An approximation due to Stoschek using powers of two and the special number 163 (the largest Heegner number) is given by
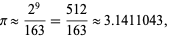 |
(79) |
which is good to 3 digits. A fraction with small numerator and denominator which gives a close approximation to 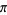 is
is
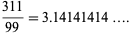 |
(80) |
Some approximations involving the ninth roots of rational numbers include
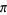 |
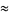 |
 |
(81) |
 |
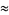 |
 |
(82) |
which are good to 12 and 15 digits, respectively (P. Galliani, pers. comm.).
de Jerphanion (pers. comm.) found
 |
(83) |
which is good to 9 digits, and J. Iuliano found
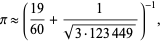 |
(84) |
which is good to 11 digits.
Definite integrals giving approximations to 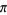 were considered by Backhouse (1995) and Lucas (2005).
were considered by Backhouse (1995) and Lucas (2005).
F. Voormanns (pers. comm., Dec. 12, 2003) found the curious astronomical approximation
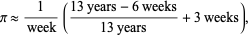 |
(85) |
which is accurate to 8 digits if the year is taken as exactly 365 days, or 6 digits if the average Gregorian year (365.2425 days) or tropical year (365.242190 days) is used.
Rivera gives other approximation formulas.
REFERENCES:
Backhouse, N. "Note 79.36. Pancake Functions and Approximations to 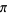 ." Math. Gaz. 79, 371-374, 1995.
." Math. Gaz. 79, 371-374, 1995.
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988a.
Castellanos, D. "The Ubiquitous Pi. Part II." Math. Mag. 61, 148-163, 1988b.
Contest Center. "Pi Competition." http://www.contestcen.com/pi.htm.
Friedman, E. "Problem of the Month (August 2004)." http://www.stetson.edu/~efriedma/mathmagic/0804.html.
Hardy, G. H. A Course of Pure Mathematics, 10th ed. Cambridge, England: Cambridge University Press, 1952.
Lucas, S. K. "Integral Proofs that 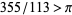 ." Gaz. Austral. Math. Soc. 32, 263-266, 2005.
." Gaz. Austral. Math. Soc. 32, 263-266, 2005.
Plouffe, S. "A Few Approximations of Pi." http://pi.lacim.uqam.ca/eng/approximations_en.html.
Ramanujan, S. "Modular Equations and Approximations to 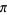 ." Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
." Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
Rivera, C. "Problems & Puzzles: Puzzle 050-The Best Approximation to Pi with Primes." http://www.primepuzzles.net/puzzles/puzz_050.htm.
Shanks, D. "Dihedral Quartic Approximations and Series for 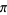 ." J. Number. Th. 14, 397-423, 1982.
." J. Number. Th. 14, 397-423, 1982.
Sloane, N. J. A. Sequences A002485/M3097, A002486/M4456, A100935, and A114526 in "The On-Line Encyclopedia of Integer Sequences."
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, 1986.



|
|
|
|
دون أهمية غذائية.. هذا ما تفعله المشروبات السكرية بالصحة
|
|
|
|
|
|
|
المنظمة العربية للطاقة تحذر من خطر.. وهذه الدولة تتميز بجودة نفطها
|
|
|
|
|
|
|
ضمن فعاليات أسبوع وليد الكعبة .. العتبة العلوية المقدسة تُقدّم فعاليات ثقافية متنوّعة عبر المنصة العلوية
|
|
|