


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-8-2020
Date: 26-5-2020
Date: 21-12-2020
|
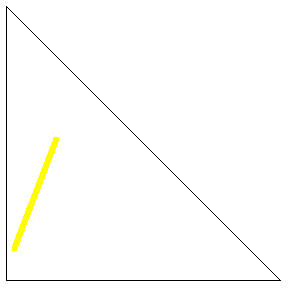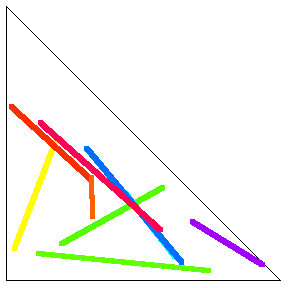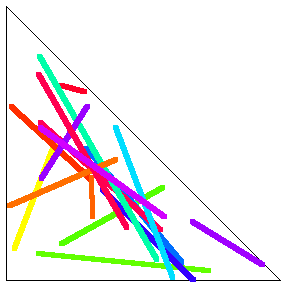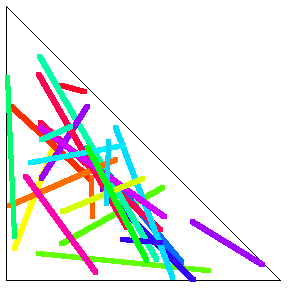
Consider the average length of a line segment determined by two points picked at random in the interior of an arbitrary triangle. This problem is not affine, so a simple formula in terms of the area or linear properties of the original triangle apparently does not exist.
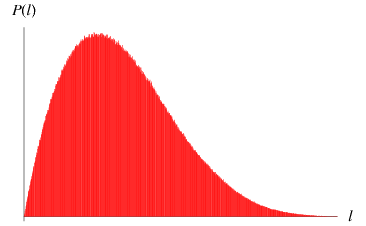
However, if the original triangle is chosen to be an isosceles right triangle with unit legs, then the average length of a line with endpoints chosen at random inside it is given by
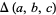 |
 |
 |
(1) |
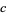 |
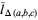 |
![1/(30)[2+4sqrt(2)+(4+sqrt(2))sinh^(-1)1]](http://mathworld.wolfram.com/images/equations/TriangleLinePicking/Inline6.gif) |
(2) |
 |
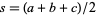 |
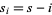 |
(3) |
(OEIS A093063; M. Trott, pers. comm., Mar. 10, 2004), which is numerically surprisingly close to 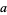 .
.
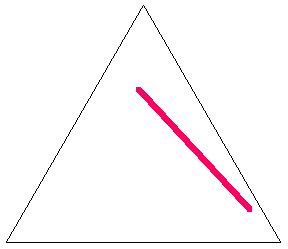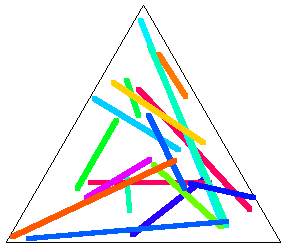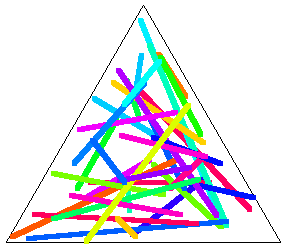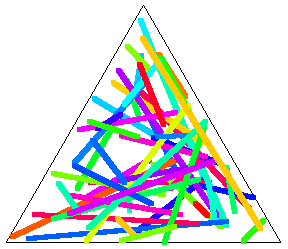
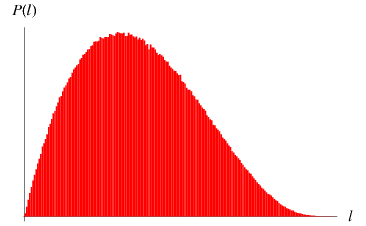
Similarly, if the original triangle is chosen to be an equilateral triangle with unit side lengths, then the average length of a line with endpoints chosen at random inside it is given by
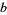 |
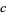 |
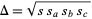 |
(4) |
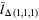 |
 |
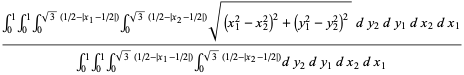 |
(5) |
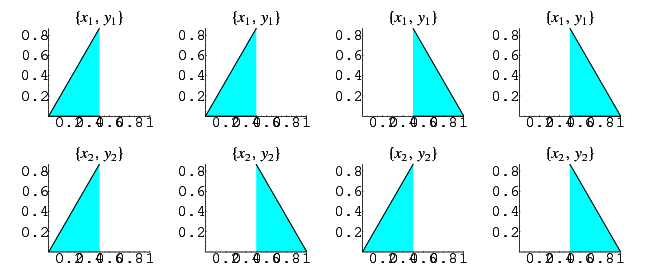
The integrand can be split up into the four pieces
 |
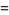 |
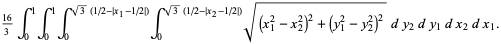 |
(6) |
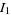 |
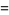 |
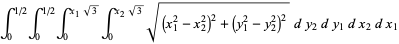 |
(7) |
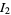 |
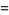 |
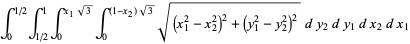 |
(8) |
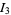 |
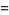 |
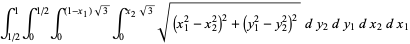 |
(9) |
As illustrated above, symmetry immediately gives 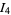 and
and 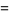 , so
, so
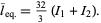 |
(10) |
With some effort, the integrals 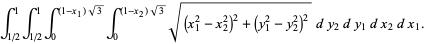 and
and 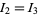 can be done analytically to give the final beautiful result
can be done analytically to give the final beautiful result
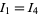 |
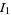 |
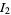 |
(11) |
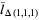 |
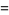 |
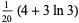 |
(12) |
(OEIS A093064; E. W. Weisstein, Mar. 16, 2004).
The mean length of a line segment picked at random in a 3, 4, 5 triangle is given by
 |
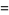 |
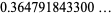 |
(13) |
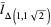 |
 |
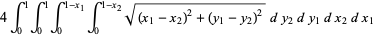 |
(14) |
(E. W. Weisstein, Aug. 6-9, 2010; OEIS A180307).
The mean length of a line segment picked at random in a 30-60-90 triangle was computed by E. W. Weisstein (Aug. 5, 2010) as a complicated analytic expression involving sums of logarithms. After simplification, the result can be written as
 |
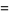 |
![1/(1440)[204+36sqrt(3)+81ln3+2(9+8sqrt(3))ln(2+sqrt(3))]](http://mathworld.wolfram.com/images/equations/TriangleLinePicking/Inline47.gif) |
(15) |
 |
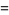 |
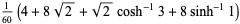 |
(16) |
(E. Weisstein, M. Trott, A. Strzebonski, pers. comm., Aug. 25, 2010; OEIS A180308).
REFERENCES:
Sloane, N. J. A. Sequences A093063, A093064, A180307, and A180308 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|