


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-7-2021
Date: 12-6-2021
Date: 1-7-2017
|
The Zariski topology is a topology that is well-suited for the study of polynomial equations in algebraic geometry, since a Zariski topology has many fewer open sets than in the usual metric topology. In fact, the only closed sets are the algebraic sets, which are the zeros of polynomials.
For example, in 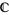 , the only nontrivial closed sets are finite collections of points. In
, the only nontrivial closed sets are finite collections of points. In 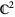 , there are also the zeros of polynomials such as lines
, there are also the zeros of polynomials such as lines 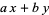 and cusps
and cusps 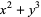 .
.
The Zariski topology is not a T2-space. In fact, any two open sets must intersect, and cannot be disjoint. Also, the open sets are dense, in the Zariski topology as well as in the usual metric topology.
Because there are fewer open sets than in the usual topology, it is more difficult for a function to be continuous in Zariski topology. For example, a continuous function 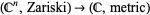 must be a constant function. Conversely, when the range has the Zariski topology, it is easier for a function to be continuous. In particular, the polynomials are continuous functions
must be a constant function. Conversely, when the range has the Zariski topology, it is easier for a function to be continuous. In particular, the polynomials are continuous functions 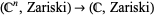 .
.
In general, the Zariski topology of a ring 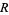 is a topology on the set of prime ideals, known as the ring spectrum. Its closed sets are
is a topology on the set of prime ideals, known as the ring spectrum. Its closed sets are 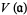 , where
, where 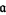 is any ideal in
is any ideal in 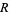 and
and 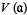 is the set of prime ideals containing
is the set of prime ideals containing 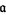 .
.
REFERENCES:
Reid, M. Undergraduate Algebraic Geometry. New York: Cambridge University Press, 1988.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|