


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-10-2019
Date: 12-8-2018
Date: 25-5-2019
|
Dyson (1962abc) conjectured that the constant term in the Laurent series
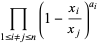 |
(1) |
is the multinomial coefficient
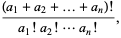 |
(2) |
based on a problem in particle physics. The theorem is called Dyson's conjecture, and was proved by Wilson (1962) and independently by Gunson (1962). A definitive proof was subsequently published by Good (1970).
A 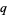 -analog of this theorem (Andrews 1975) states that the coefficient of
-analog of this theorem (Andrews 1975) states that the coefficient of 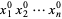 in
in
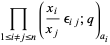 |
(3) |
where
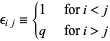 |
(4) |
is given by
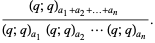 |
(5) |
This can also be stated in the form that the constant term of
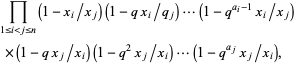 |
(6) |
is the q-multinomial coefficient
![([a_1+...+a_n]!)/([a_1]!...[a_n]!),](http://mathworld.wolfram.com/images/equations/Zeilberger-BressoudTheorem/NumberedEquation7.gif) |
(7) |
where ![[n]!](http://mathworld.wolfram.com/images/equations/Zeilberger-BressoudTheorem/Inline3.gif) is the q-factorial. The amazing proof of this theorem was given by Zeilberger and Bressoud (1985).
is the q-factorial. The amazing proof of this theorem was given by Zeilberger and Bressoud (1985).
The full theorem reduces to Dyson's version when 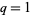 . It also gives the q-analog of Dixon's theorem as
. It also gives the q-analog of Dixon's theorem as
![sum_(k=-infty)^infty(-1)^kq^(k(3k+1)/2)[b+c; c+k]_q[c+a; a+k]_q[a+b; b+k]_q
=((q;q)_(a+b+c))/((q;q)_a(q;q)_b(q;q)_c)](http://mathworld.wolfram.com/images/equations/Zeilberger-BressoudTheorem/NumberedEquation8.gif) |
(8) |
(Andrews 1975, 1986), where ![[n; k]_q](http://mathworld.wolfram.com/images/equations/Zeilberger-BressoudTheorem/Inline5.gif) is a q-binomial coefficient. With
is a q-binomial coefficient. With 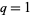 and
and 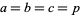 , it gives the beautiful and well-known identity
, it gives the beautiful and well-known identity
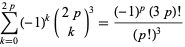 |
(9) |
(Andrews 1986).
REFERENCES:
Andrews, G. E. "Problems and Prospects for Basic Hypergeometric Functions." In The Theory and Application of Special Functions (Ed. R. Askey). New York: Academic Press, pp. 191-224, 1975.
Andrews, G. E. "The Zeilberger-Bressoud Theorem." §4.3 in q-Series: Their Development and Application in Analysis, Number Theory, Combinatorics, Physics, and Computer Algebra. Providence, RI: Amer. Math. Soc., pp. 36-38, 1986.
Dyson, F. "Statistical Theory of the Energy Levels of Complex Systems. I." J. Math. Phys. 3, 140-156, 1962a.
Dyson, F. "Statistical Theory of the Energy Levels of Complex Systems. II." J. Math. Phys. 3, 157-165, 1962b.
Dyson, F. "Statistical Theory of the Energy Levels of Complex Systems. III." J. Math. Phys. 3, 166-175, 1962c.
Good, I. J. "Short Proof of a Conjecture by Dyson." J. Math. Phys. 11, 1884, 1970.
Gunson, J. "Proof of a Conjecture of Dyson in the Statistical Theory of Energy Levels." J. Math. Phys. 3, 752-753, 1962.
Wilson, K. G. "Proof of a Conjecture by Dyson." J. Math. Phys. 3, 1040-1043, 1962.
Zeilberger, D. and Bressoud, D. M. "A Proof of Andrews' 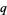 -Dyson Conjecture." Disc. Math. 54, 201-224, 1985.
-Dyson Conjecture." Disc. Math. 54, 201-224, 1985.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|