


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-5-2018
Date: 27-4-2018
Date: 21-8-2019
|
Denote the 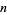 th derivative
th derivative 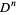 and the
and the 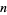 -fold integral
-fold integral 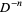 . Then
. Then
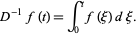 |
(1) |
Now, if the equation
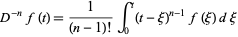 |
(2) |
for the multiple integral is true for 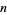 , then
, then
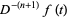 |
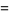 |
![D^(-1)[1/((n-1)!)int_0^t(t-xi)^(n-1)f(xi)dxi]](http://mathworld.wolfram.com/images/equations/FractionalIntegral/Inline8.gif) |
(3) |
 |
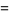 |
![int_0^t[1/((n-1)!)int_0^x(x-xi)^(n-1)f(xi)dxi]dx.](http://mathworld.wolfram.com/images/equations/FractionalIntegral/Inline11.gif) |
(4) |
Interchanging the order of integration gives
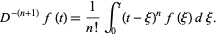 |
(5) |
But (3) is true for 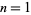 , so it is also true for all
, so it is also true for all 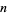 by induction. The fractional integral of
by induction. The fractional integral of 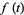 of order
of order 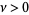 can then be defined by
can then be defined by
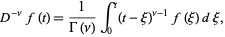 |
(6) |
where 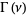 is the gamma function.
is the gamma function.
More generally, the Riemann-Liouville operator of fractional integration is defined as
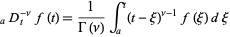 |
(7) |
for 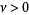 with
with 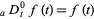 (Oldham and Spanier 1974, Miller and Ross 1993, Srivastava and Saxena 2001, Saxena 2002).
(Oldham and Spanier 1974, Miller and Ross 1993, Srivastava and Saxena 2001, Saxena 2002).
The fractional integral of order 1/2 is called a semi-integral.
Few functions have a fractional integral expressible in terms of elementary functions. Exceptions include
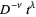 |
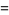 |
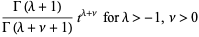 |
(8) |
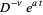 |
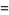 |
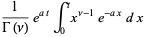 |
(9) |
 |
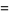 |
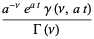 |
(10) |
 |
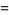 |
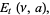 |
(11) |
where 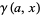 is a lower incomplete gamma function and
is a lower incomplete gamma function and 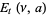 is the Et-function. From (10), the fractional integral of the constant function
is the Et-function. From (10), the fractional integral of the constant function 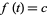 is given by
is given by
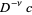 |
 |
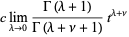 |
(12) |
 |
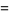 |
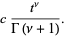 |
(13) |
A fractional derivative can also be similarly defined. The study of fractional derivatives and integrals is called fractional calculus.
REFERENCES:
Miller, K. S. and Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations. New York: Wiley, 1993.
Oldham, K. B. and Spanier, J. The Fractional Calculus: Integrations and Differentiations of Arbitrary Order. New York: Academic Press, 1974.
Samko, S. G.; Kilbas, A. A.; and Marichev, O. I. Fractional Integrals and Derivatives. Yverdon, Switzerland: Gordon and Breach, 1993.
Saxena, R. K.; Mathai, A. M.; and Haubold, H. J. "On Fractional Kinetic Equations." 23 Jun 2002. http://arxiv.org/abs/math.CA/0206240.
Srivastava, H. M. and Saxena, R. K. "Operators of Fractional Integration and Their Applications." Appl. Math. and Comput. 118, 1-52, 2001.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|