


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-5-2019
Date: 13-8-2018
Date: 15-5-2018
|
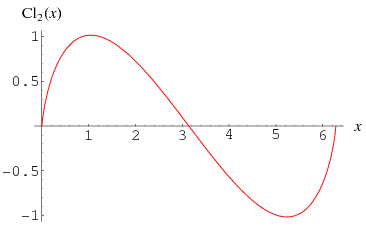
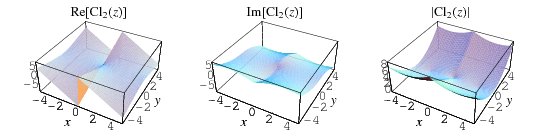
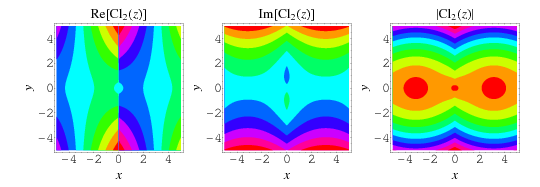
Clausen's integral, sometimes called the log sine integral (Borwein and Bailey 2003, p. 88) is the 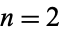 case of the
case of the 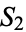 Clausen function
Clausen function
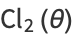 |
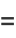 |
![-int_0^thetaln[2sin(1/2t)]dt](http://mathworld.wolfram.com/images/equations/ClausensIntegral/Inline5.gif) |
(1) |
 |
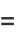 |
![i(1/6pi^2-1/4x^2)+x[ln(1-e^(ix))-ln2]-iLi_2(e^(ix))-xln[sin(1/2x)],](http://mathworld.wolfram.com/images/equations/ClausensIntegral/Inline8.gif) |
(2) |
where 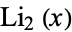 is a dilogarithm.
is a dilogarithm.
Clausen's integral has the special value
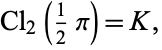 |
(3) |
where 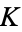 is Catalan's constant (Borwein and Bailey 2003, p. 89). Other identities include
is Catalan's constant (Borwein and Bailey 2003, p. 89). Other identities include
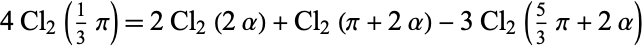 |
(4) |
where 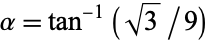 ,
,
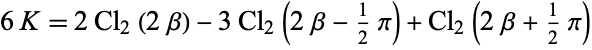 |
(5) |
where 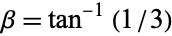 , and
, and
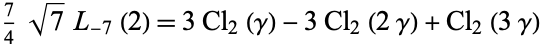 |
(6) |
where 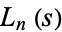 is a Dirichlet L-series and
is a Dirichlet L-series and 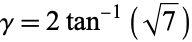 (Borwein and Bailey 2003, pp. 89-90).
(Borwein and Bailey 2003, pp. 89-90).
BBP-type formulas include
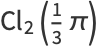 |
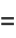 |
![sqrt(3)sum_(k=0)^(infty)[1/((6k+1)^2)+1/((6k+2)^2)-1/((6k+4)^2)-1/((6k+5)^2)]](http://mathworld.wolfram.com/images/equations/ClausensIntegral/Inline17.gif) |
(7) |
 |
 |
![(sqrt(3))/9sum_(k=0)^(infty)((-1)^k)/(27^k)[(18)/((6k+1)^2)-(18)/((6k+2)^2)-(24)/((6k+3)^2)-6/((6k+4)^2)+2/((6k+5)^2)]](http://mathworld.wolfram.com/images/equations/ClausensIntegral/Inline20.gif) |
(8) |
(Bailey 2000, Borwein and Bailey 2003, pp. 128-129).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 1005-1006, 1972.
Ashour, A. and Sabri, A. "Tabulation of the Function 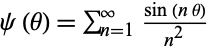 ." Math. Tables Aids Comp. 10, 54 and 57-65, 1956.
." Math. Tables Aids Comp. 10, 54 and 57-65, 1956.
Bailey, D. H. "A Compendium of BBP-Type Formulas for Mathematical Constants." 28 Nov 2000. http://crd.lbl.gov/~dhbailey/dhbpapers/bbp-formulas.pdf.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 89-90, 2003.
Clausen, R. "Über die Zerlegung reeller gebrochener Funktionen." J. reine angew. Math. 8, 298-300, 1832.
Lewin, L. "Clausen's Integral." Ch. 4 in Dilogarithms and Associated Functions. London: Macdonald, pp. 91-105, 1958.
Lewin, L. Polylogarithms and Associated Functions. New York: North-Holland, 1981.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|