Bell Polynomial

There are two kinds of Bell polynomials.

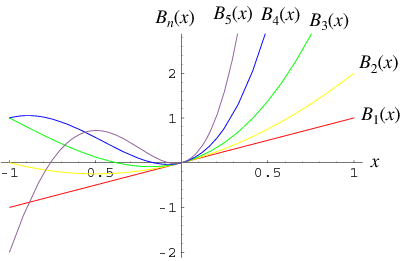
A Bell polynomial 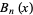, also called an exponential polynomial and denoted  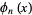(Bell 1934, Roman 1984, pp. 63-67) is a polynomial  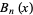that generalizes the Bell number  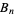and complementary Bell number  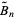such that

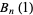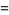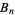			(1)
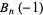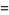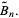			(2)

These Bell polynomial generalize the exponential function.

Bell polynomials should not be confused with Bernoulli polynomials, which are also commonly denoted .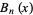

Bell polynomials are implemented in the Wolfram Language as BellB[n, x].

The first few Bell polynomials are

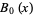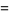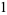			(3)
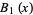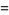			(4)
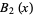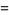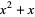			(5)
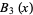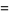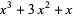			(6)
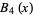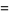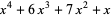			(7)
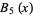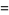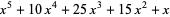			(8)
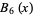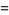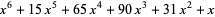			(9)

(OEIS A106800).

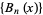 forms the associated Sheffer sequence for

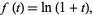(10)

so the polynomials have that exponential generating function

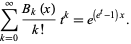(11)

Additional generating functions for 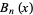 are given by

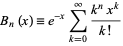(12)

or

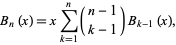(13)

with 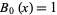, where  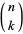is a binomial coefficient.

The Bell polynomials 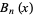 have the explicit formula

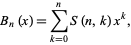(14)

where 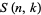 is a Stirling number of the second kind.

A beautiful binomial sum is given by

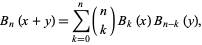(15)

where 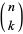 is a binomial coefficient.

The derivative of 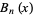 is given by

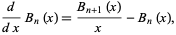(16)

so 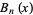 satisfies the recurrence equation

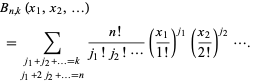(17)

The second kind of Bell polynomials 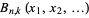 are defined by

They have generating function

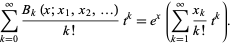(18)

REFERENCES:

Bell, E. T. "Exponential Polynomials." Ann. Math. 35, 258-277, 1934.

Comtet, L. Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, p. 133, 1974.

Riordan, J. An Introduction to Combinatorial Analysis. New York: Wiley, pp. pp. 35-38, 49, and 142, 1980.

Roman, S. "The Exponential Polynomials" and "The Bell Polynomials." §4.1.3 and §4.1.8 in The Umbral Calculus. New York: Academic Press, pp. 63-67 and 82-87, 1984.

Sloane, N. J. A. Sequence A106800 in "The On-Line Encyclopedia of Integer Sequences."