


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-9-2018
Date: 30-3-2019
Date: 21-5-2019
|
For a set of  numbers or values of a discrete distribution
numbers or values of a discrete distribution  , ...,
, ...,  , the root-mean-square (abbreviated "RMS" and sometimes called the quadratic mean), is the square root of mean of the values
, the root-mean-square (abbreviated "RMS" and sometimes called the quadratic mean), is the square root of mean of the values  , namely
, namely
 |
 |
 |
(1) |
 |
 |
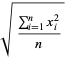 |
(2) |
 |
 |
 |
(3) |
where  denotes the mean of the values
denotes the mean of the values  .
.
For a variate  from a continuous distribution
from a continuous distribution  ,
,
![x_(RMS)=sqrt((int[P(x)]^2dx)/(intP(x)dx)),](http://mathworld.wolfram.com/images/equations/Root-Mean-Square/NumberedEquation1.gif) |
(4) |
where the integrals are taken over the domain of the distribution. Similarly, for a function  periodic over the interval
periodic over the interval  ], the root-mean-square is defined as
], the root-mean-square is defined as
![f_(RMS)=sqrt(1/(T_2-T_1)int_(T_1)^(T_2)[f(t)]^2dt).](http://mathworld.wolfram.com/images/equations/Root-Mean-Square/NumberedEquation2.gif) |
(5) |
The root-mean-square is the special case  of the power mean.
of the power mean.
Hoehn and Niven (1985) show that
 |
(6) |
for any positive constant  .
.
Physical scientists often use the term root-mean-square as a synonym for standard deviation when they refer to the square root of the mean squared deviation of a signal from a given baseline or fit.
REFERENCES:
Hoehn, L. and Niven, I. "Averages on the Move." Math. Mag. 58, 151-156, 1985.
Kenney, J. F. and Keeping, E. S. "Root Mean Square." §4.15 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 59-60, 1962.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|