Carleman's Inequality

Let 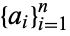 be a set of positive numbers. Then

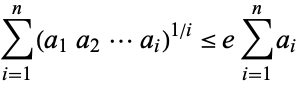(which is given incorrectly in Gradshteyn and Ryzhik 2000). Here, the constant e is the best possible, in the sense that counterexamples can be constructed for any stricter inequality which uses a smaller constant. The theorem is suggested by writing 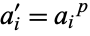in Hardy's inequality

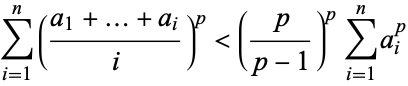and letting .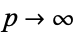

REFERENCES:

Carleman, T. "Sur les fonctions quasi-analytiques." Conférences faites au cinqui'eme congrès des mathématiciens scandinaves. Helsingfors, pp. 181-196, 1923.

Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. 1126, 2000.

Hardy, G. H.; Littlewood, J. E.; and Pólya, G. "Carleman's Inequality." §9.12 in Inequalities, 2nd ed. Cambridge, England: Cambridge University Press, pp. 249-250, 1988.

Kaluza, T. and Szegö, G. "Über Reihen mit lauter positiven Gliedern." J. London Math. Soc. 2, 266-272, 1927.

Knopp, K. "Über Reihen mit positiven Gliedern." J. London Math. Soc. 3, 205-211, 1928.

Mitrinović, D. S. Analytic Inequalities. New York: Springer-Verlag, p. 131, 1970.

Ostrowski, A. "Über quasi-analytischen Funktionen und Bestimmtheit asymptotischer Entwicklungen." Acta Math. 53, 181-266, 1929.

Pólya, G. "Proof of an Inequality." Proc. London Math. Soc. 24, lvii, 1926.

Valiron, G. §3, Appendix B in Lectures on the General Theory of Integral Functions. New York: Chelsea, pp. 186-187, 1949.