


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-4-2018
Date: 17-9-2019
Date: 2-5-2019
|
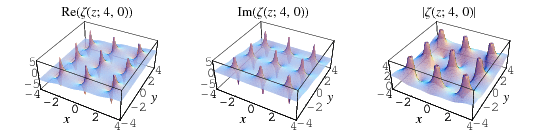
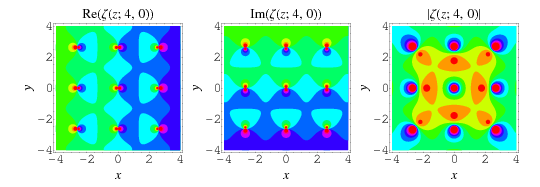
The Weierstrass zeta function 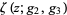 is the quasiperiodic function defined by
is the quasiperiodic function defined by
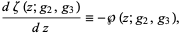 |
(1) |
where 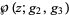 is the Weierstrass elliptic function with invariants
is the Weierstrass elliptic function with invariants 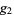 and
and 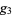 , with
, with
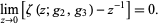 |
(2) |
As in the case of other Weierstrass elliptic functions, the elliptic invariants 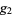 and
and 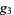 are frequently suppressed for compactness. The function is implemented in the Wolfram Language as WeierstrassZeta[u,
are frequently suppressed for compactness. The function is implemented in the Wolfram Language as WeierstrassZeta[u, 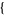 g2, g3
g2, g3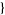 ].
].
Using the definition above gives
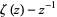 |
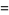 |
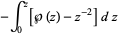 |
(3) |
 |
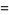 |
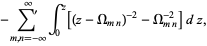 |
(4) |
where 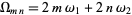 , so
, so
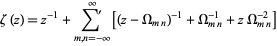 |
(5) |
so 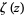 is an odd function. Integrating
is an odd function. Integrating 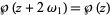 gives
gives
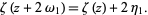 |
(6) |
Letting 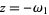 gives
gives
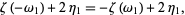 |
(7) |
so
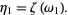 |
(8) |
Similarly,
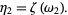 |
(9) |
From Whittaker and Watson (1990),
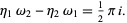 |
(10) |
If 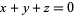 , then
, then
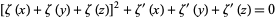 |
(11) |
(Whittaker and Watson 1990, p. 446). Also,
 |
(12) |
(Whittaker and Watson 1990, p. 446).
The series expansion of 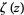 is given by
is given by
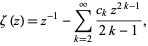 |
(13) |
where
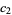 |
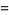 |
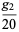 |
(14) |
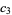 |
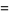 |
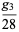 |
(15) |
and
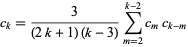 |
(16) |
for 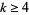 (Abramowitz and Stegun 1972, p. 635). The first few coefficients are therefore
(Abramowitz and Stegun 1972, p. 635). The first few coefficients are therefore
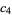 |
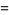 |
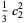 |
(17) |
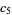 |
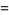 |
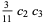 |
(18) |
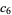 |
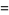 |
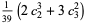 |
(19) |
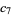 |
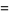 |
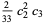 |
(20) |
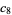 |
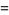 |
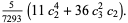 |
(21) |
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). "Weierstrass Elliptic and Related Functions." Ch. 18 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, pp. 627-671, 1972.
Brezhnev, Y. V. "Uniformisation: On the Burnside Curve 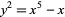 ." 9 Dec 2001. http://arxiv.org/abs/math.CA/0111150.
." 9 Dec 2001. http://arxiv.org/abs/math.CA/0111150.
Tölke, F. "Spezielle Weierstraßsche Zeta-Funktionen." Ch. 8 in Praktische Funktionenlehre, dritter Band: Jacobische elliptische Funktionen, Legendresche elliptische Normalintegrale und spezielle Weierstraßsche Zeta- und Sigma Funktionen. Berlin: Springer-Verlag, pp. 145-163, 1967.
Whittaker, E. T. and Watson, G. N. "Quasi-Periodic Functions. The Function 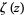 " and "The Quasi-Periodicity of the Function
" and "The Quasi-Periodicity of the Function 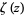 ." §20.4 and 20.41 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 445-447 and 449-451, 1990.
." §20.4 and 20.41 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 445-447 and 449-451, 1990.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|